|
ОПРЕДЕЛЕНИЕ
Индекс товарного канала (CCI) измеряет отклонение цены бумаги от ее среднестатистической цены. Высокие значения индекса указывают на то, что цена необычно высока по сравнению со средней, а низкие – что она слишком занижена. Несмотря на название, CCI применим к любому финансовому инструменту, а не только к товарам.


CCI разработал Дональд Ламберт (Donald Lambert).
ИНТЕРПРЕТАЦИЯ
Существует два основных способа использования CCI: для поиска расхождений и в качестве индикатора перекупленности/перепроданности.
• Расхождение (см. стр. 30) образуется, когда цена достигает нового максимума, а CCI не удается подняться выше предыдущих максимумов. За этим классическим расхождением обычно следует ценовая коррекция.
• CCI обычно колеблется в диапазоне ±100. Значения выше +100 говорят о состоянии перекупленности (и вероятности корректирующего спада), а значения ниже 100 – о состоянии перепроданности (и вероятности корректирующего подъема).
ПРИМЕР
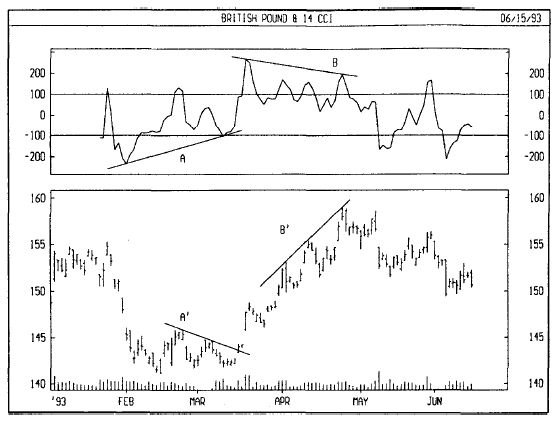
На следующем рисунке показаны графики курса британского фунта и 14дневного CCI. В области А образовалось бычье расхождение (цены падали, а CCI повышался), за которым последовал подъем цен. В области В возникло медвежье расхождение (цены росли при одновременном падении CCI). В результате произошел корректирующий спад. Заметьте, что эти расхождения образовались в областях экстремальных значений индикатора (ниже 100 и выше +100), что придает им дополнительную значимость.
РАСЧЕТ
Исчерпывающее объяснение процедуры расчета CCI выходит за рамки этой книги. Ниже описаны лишь основные ее этапы:
1. Сложите максимум, минимум и цену закрытия каждого периода и разделите сумму на 3. Полученное значение называется типичной ценой (см. стр. 189).
2. Вычислите n-периодное простое скользящее среднее типичных цен, полученных по п. 1.
3. Вычтите полученное по п. 2 значение для текущего периода из типичных цен (п. 1) каждого из предшествующих n периодов. Например, при расчете 5дневного CCI нужно найти пять значений разности с сегодняшним значением, полученным по п. 2.
4. Вычислите n периодное простое скользящее среднее абсолютных значений каждой из величин, полученных по п. 3.
5. Умножьте полученное по п.4 значение на 0,015.
6. Из полученного по п. 1 значения вычтите значение, полученное по п. 2.
7. Разделите значение по п. 6 на значение по п. 5.
|



















