|
«За исключением цифр, нет ничего более обманчивого, чем факты»
Адам Смит, шотландский экономист
Ключевым моментом процесса принятия инвестиционных решений является определение двух, типов ошибок – ошибки I и II рода.


Так, мы можем не купить товар, который будет дорожать или же купить товар, который на самом деле не будет расти в цене. И в первом и во втором случае принятое инвестиционное решение будет являться ошибочным. Соответственно это будут ошибки первого и второго рода.

Оба типа ошибок самым непосредственным образом отражаются на состоянии инвестиционного счета. При этом наиболее типичной ошибкой является ошибка II рода, однако наиболее значимой является ошибка I рода, т.е. получение убытков. Данной ошибки стремятся избегать в первую очередь, жертвуя при этом стремительным и неизбежным ростом количества ошибок II рода.
Вероятность допущения ошибки I рода называется уровнем значимости.
Бывает один или два уровня значимости. Зависит их количество от постановки задачи проверки гипотезы – вы можете провести двустороннюю или одностороннюю проверку. Первая обладает двумя, а вторая одним уровнями значимости. Односторонняя проверка и соответственно один критерий значимости используются, когда необходимо оценить, является ли фактическое значение анализируемого параметра строго больше или меньше установленного уровня значимости. Графически соблюдение одного уровня значимости (правостороннего, когда необходимо, чтобы анализируемый параметр был строго больше уровня значимости) выглядит, как это показано на следующем рисунке.
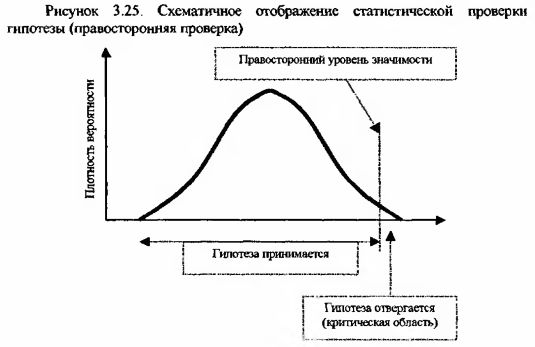
Когда необходимо просто оценить, отличается ли реальное значение анализируемого параметра от фактического, применяется двусторонняя проверка и соответственно два уровня значимости. Графически соблюдение двух уровней значимости выглядит, как это показано на следующем рисунке.
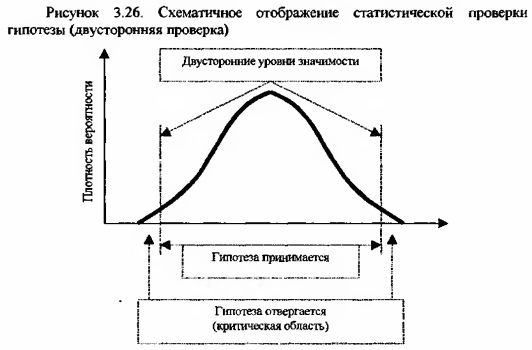
Обычно выделяют уровни значимости в 0.1%, 1% или 5%. Если расчетное значение анализируемого параметра (фактическая вероятность допущения ошибки) меньше 5%, то гипотеза может быть явно неверной. Если найденная вероятность меньше 1%, то гипотеза неверна. Если же вероятность меньше 0.1%, то гипотеза практически наверняка неверна.
Например.
1. Представим себе, что мы поддерживаем теорию случайного блуждания цен и решили еще раз удостовериться в истинности этой теории. Выдвинем гипотезу о том, что ежедневное изменение (закрытие к закрытию) фондового индекса DJI является случайной величиной со всеми вытекающими отсюда последствиями.
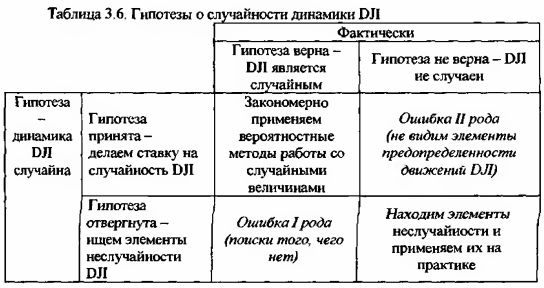
Проанализируем ряд значений DJI за период с января 1915г. по октябрь 1999г. (20757 торговых дня). Примем, что рост индекса DJI (закрытие текущего дня выше последнего значения предыдущей торговой сессии) мы будем обозначать как +1, а снижение как -1. Тогда окажется, что за этот период было 10945 растущих дней и 9812 падающих, что соответственно составляет 52.7% и 47.3% от общего количества рассмотренных торговых сессий. Эти значения очень близки к вероятности выпадения орлов или решек, которое можно наблюдать при подбрасывании монеты. Однако это только ощущение, которое еще нужно статистически подтвердить.
2. Разница между полученным фактическим значением вероятности появления «медвежьего» дня и теоретическим его значением составляет 2.7% (50% – 47.3%). Уровень значимости или вероятностью ошибки I рода для приведенной выше таблицы, таким образом, составляет 5.4% (2.7% * 2). Столь низкое значение уровня, близкое к академическим 5%, как мы знаем, говорит о том, что гипотеза о случайности рынка может быть принята.
3. Итак, допустим, что положительные и отрицательные изменения индекса DJI чередуются случайным образом. Фактическая вероятность случайного изменения равна теоретической: в любой момент времени вероятность появления +1 или -1 близка к 0.5. В этом случае вероятность серий из двух, трех и более подряд изменений фондового индекса будет выглядеть, как это показано на следующем рисунке.
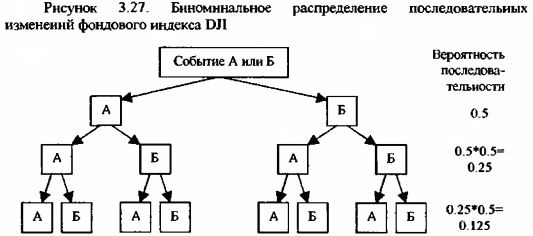
Здесь событие А соответствует росту индекса, а Б его падению. Тогда вероятность последовательности AAA, также как и любой другой последовательности из трех подряд изменений фондового индекса (АБА, ББА и т.п.) равна 0.125:
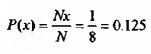
Так ли это?
Прежде чем ответить утвердительно на этот вопрос, на что нас подталкивает знание теории вероятностей, давайте разгадаем следующую задачку:
Какой ряд, по вашему мнению, более похож на случайную последовательность:
АБАААБББАБААБББАААБАБ
АБАБАБББААБАБАББАААБА
В этом примере каждая серия содержит 11 букв «А» и 10 букв «Б». В первой серии вероятность смены знака равна 50% (смена букв произошла в 10 случаях из 20, что соответствует случайной последовательности), а во втором – 70% (смена букв произошла в 14 случаях из 20, что значительно чаще ожидаемого в случайном наборе букв). Первый ряд, таким образом, имеет более случайный вид, нежели второй.
Из регрессии к среднему мы знаем, что частая смена последовательности (например А-Б-А-Б-А-...) событий или знаков, также как и редкая смена последовательности (А-А-А-А-Б-Б-Б-...), отклоняющаяся в первом случае от нормального 0.5 к 1 и втором – от 0.5 к 0, являются маловероятными на продолжительном промежутке времени и существуют только на коротком.
Для расчетов используем закон малых чисел. Применительно к анализу статистических рядов динамики цен закон малых чисел – это вера в то, что выбранная наугад последовательность чисел будет иметь более случайный вид, чем это есть на самом деле. Т.е. если вы попробуете записать предполагаемую последовательность подбрасываний монетки с двумя исходами – орел или решка, то она в вашей интерпретации, скорее всего, будет иметь более случайный вид, нежели фактическое подбрасывание. Мы стремимся не отмечать длинные очереди орлов (или решек), переоценивая случайный фактор. Здесь же кроется ошибка начинающих трейдеров, склонных недооценивать случайное блуждание рыночных цен (например, последовательный десятидневный рост). В итоге это приводит к завышенным ожиданиям быстрой остановки тренда, переоценке шансов осцилляторов к скорейшему развороту, т.е. к ожиданиям большей «нормальности» рынка, чем это ему присуще.
Из психологии известно, что люди склонны видеть закономерности в случайных событиях. Однако люди, как правило, умеют отличать случайные ряды от рядов с определенной закономерностью (если они представлены как две альтернативы). В целом же люди видят случайность там, где присутствует структура (ошибка II рода), и структуру там, где была случайность (ошибка I рода). Люди имеют предубеждение против длинных рядов повторений, считая их порождением неких закономерностей. Подготовка в анализе и определении случайных рядов существенно улучшает результат по их распознаванию.
Еще один интересный пример, характерный для вероятностных рядов.
В каждом круге игры 20 монет распределяются случайным образом среди пяти игроков. Вам предъявлены два типа распределений:

Если кругов игры много, какого типа результатов будет больше – типа I или типа II?
Большинство выбирает распределение I, так как люди думают, что «случайное» распределение должно быть хаотичным и бессистемным. Распределение типа II кажется при этом слишком упорядоченным.
Дополняет этот пример еще один.
Оцените, равны ли вероятиости появления 10 «бычьих» дней из 15 торговых сессий и 100 «бычьих» дней из 150 торговых сессий для фондового индекса DJI.
Большинство людей скажут, что вероятности этих событий равны. Однако, если исходить из фактических данных распределения динамики фондового индекса, близкого к нормальному, то можно заметить, что вероятность первого события выше, чем второго. Это происходит из-за разных объемов выборки: чем больше выборка, тем больше вероятность приближения результатов распределения к нормальному.
Здесь же стоит сказать еще об одном правиле теории вероятностей, часто называемом первой теоремой. Данная теорема исходит из анализа кривой случайных блужданий.
Случайным блужданием называется такое изменение переменной i, для которой верно следующее:
- существует всего две возможности для перехода из одной точки в другую;
- переход из одной точки в другую происходит по целочисленным значениям (например, +/-1);
- суммарная вероятность переходов в два возможных других состояния равна 1 (если вероятность перехода в первое состояние равна p, то вероятность перехода во второе состояние равна p = 1 – q);
- переход из одного состояния в другое происходит независимо от прошлого.
Ниже приведен пример такого случайного блуждания, который отражает последовательный переход переменной в два возможных состояния +1 или -1 с равной вероятностью 0.5. Накопленный результат 4.5 миллионов последовательных переходов приведен на рисунке.
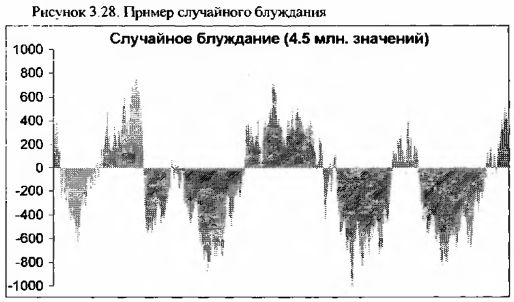
Как мы видим, даже при таком большом количестве переходов кривая случайного блуждания не является строго правильной. Если мы обозначим через +1 прибыль, а через -1 убытки, то можно сделать следующие интересные и важные выводы:
- рано или поздно состояние прибыли (зона выше 0) сменяется состоянием убытков (зона меньше 0), и наоборот. Из этого следует, что стоит только подождать и вслед за «темной» зоной обязательно последуют «ясные» дни. Однако отсюда же можно сделать вывод о том, что после получения прибыли ждите неминуемых убытков;
- с увеличением количества переходов мы не наблюдаем сходимости кривой к 0, что не подтверждает правила – чем дольше играешь, тем с большей вероятностью прибыли должны соответствовать убыткам, а суммарный финансовый результат стремиться к нолю. Таким образом, можно говорить о том. что финансовый результат такой игры в очень редкие моменты будет близок или равен нолю, а все остальное время вас будет «бросать то в жар, то в холод»;
- количество и время прибыльных и убыточных зон также являются случайными и непредсказуемыми величинами;
- чем больший ряд случайных блужданий исследуется, тем ближе распределение его вероятностей к нормальному (при условии вероятностей переходов равными 0.5);
- распределение вероятностей в каждой отдельной конечной серии переходов, скорее всего, будет далеко от нормального. И тем дальше оно будет, чем меньший ряд исследуется;
- знание прошлых данных действительно совершенно не помогает в оценке будущих событий, даже таких общих как, например, количество и смена победных и проигрышных серий.
А теперь снова вернемся к нашей гипотезе о том, что динамика фондового индекса DJI является случайной величиной.
Если проанализировать ряд значений индекса DJI (дневные close), учитывая только простые положительные или отрицательные изменения этих значений с января 1915г по октябрь 1999г. (ряд из 20757 дней), то можно сделать вывод о том, насколько случайна последовательность значений индекса. Смена знака произошла в 10596 случаях из 20757, что соответствует 51%-ной вероятности и практически точно соответствует случайной последовательности смены знаков.
Однако если рассматривать более короткие ряды данных за этот же период времени (например, по 50-100 рабочих дней подряд), то последовательности представляются не столь уж и случайными. Периоды высокой волатильности рынка (значительной изменчивости индекса DJI с достижением частоты смены знаков 60-70%%) сочетались с периодами трендового движения (низкой изменчивости DJI при частоте 30-40%%). Этот факт еще раз подтверждает наличие краткосрочных отклонений от общей случайности поведения рынка и эффекта сходимости к средней.
В продолжение процесса проверки, является ли случайной последовательностью ряд изменений фондового индекса DJI, определим данные о непрерывных сериях +1 и -1, которые были присуши для значений фондового индекса DJI в течение анализируемого периода.
За это время можно было наблюдать непрерывные серии в 13 растущих дней и 12 подающих дней подряд, а полная раскладка непрерывных серий приведена в следующей таблице.
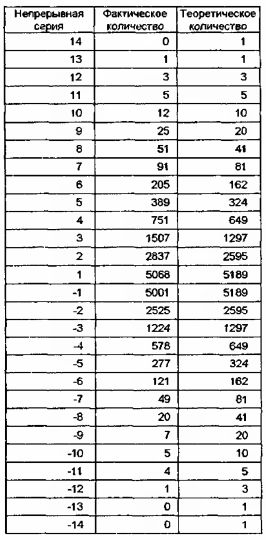
Как мы видим, разница между фактическими и теоретическими значениями, рассчитанными исходя из равновероятного исхода последовательностей (см. рисунок 3.27), настолько мала, что эти два ряда значений практически точно соответствуют друг другу.
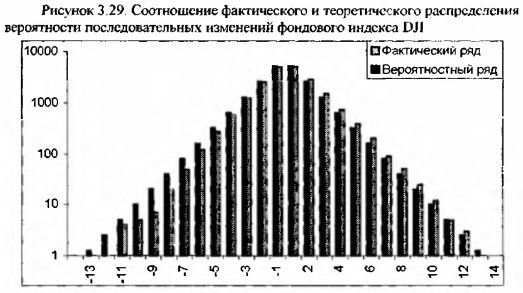
Графически приведенные в таблице значения фактического ряда выглядят очень даже красиво и напоминают не что иное как нормальное распределение с центром возле 0.
Стандартное отклонение разницы между этими двумя рядами составляет 84. Это очень низкое значение, которое усиливает тезис о случайности изменений фондового индекса DJI.
Дополнительный интерес может представлять разница между значениями фактического и вероятностного рядов, для наглядности рассчитанная в %.

Здесь видно, что в области отрицательных серий, т.е. серий непрерывных падений фондового индекса DJI наблюдается расхождение в сторону вероятностного ряда – значения вероятностного ряда больше значений фактического ряда непрерывных серий. С другой стороны, в области положительной области, т.е. серий непрерывного роста фондового индекса DJI наблюдается расхождение в сторону ряда фактических значении – значения вероятностного ряда меньше значений фактического ряда непрерывных серий. Это означает, что серии роста фондового индекса на практике встречаются чаще, чем этого можно было бы ожидать. С другой стороны, серии падения фондового индекса встречаются реже, чем этого можно было бы ожидать. Думаю, именно этим можно объяснить долгосрочную тенденцию роста фондового индекса DJI. С фундаментальной точки зрения индекс DJI обречен на рост, пока экономика США будет расширяться, на что будет указывать увеличение реального, с учетом инфляции ВВП.
Стандартное отклонение для ряда фактического количества непрерывных серий составляет 2.45, а его средневзвешенное значение 2. На основании этих цифр можно сделать следующие выводы:
- с вероятностью 87.09% (теоретическое нормативное значение 68.27%) в этом периоде непрерывные серии составляли от 5 растущих до 2 падающих дней подряд (2 + 3 (округление до большего 2.45));
- с вероятностью 97.20% (теоретическое значение 95.45%) непрерывные серии находились в интервале от 7 растущих до 4 падающих дней подряд (2 + 5 (округление до большего 2.45 * 2 = 4.90));
- с вероятностью 99.78% (теоретическое значение 99.73%) непрерывные серии находились в интервале от 10 растущих до 7 падающих дней подряд (2 +/- 8 (округление до большего 2.45 * 3 = 7.35)).
Как результат, если вы наблюдаете 8 подряд падающих дней, то можете с очень большой долей уверенности, измеряющейся приблизительной величиной 99.78%, сделать ставку на рост фондового индекса DJI.
Похожие результаты мы наблюдаем для непрерывных серий значений фондового индекса DJI, где взяты не абсолютные (+1 и -1), а процентные изменения этих значений, что является более качественной оценкой непрерывных серий.
Стандартное отклонение для процентного ряда составляет 1.6%, а средняя 0%. На основании этих цифр можно сделать следующие выводы:
- с вероятностью 80.25% (теоретическое значение 68.27%) в этом периоде непрерывные серии находились в интервале от +1.6% до -1.6%;
- с вероятностью 93.42% (теоретическое значение 95.45%) непрерывные серии находились в интервале от +3.2% до -3.2%;
- с вероятностью 97.56% (теоретическое значение 99.73%) непрерывные серии находились в интервале от +4.8% до -4.8%.
Как результат, если вы наблюдаете рост или падение фондового индекса на 4.8% в течение одной или нескольких торговых сессий подряд (рассчитано по ценам закрытия), то можете с очень большой долей уверенности, измеряющейся приблизительной величиной 97.56%, сделать ставку на рост фондового индекса DJI.
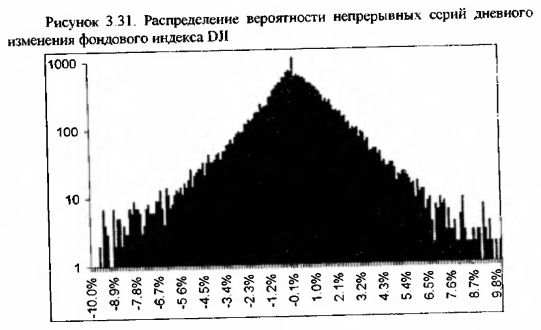
Исходя из приведенных выше рисунков, на которых запечатлены непрерывные серии, можно сделать предположение о том, что динамика фондового индекса DJI подчиняется закону нормального распределения. Это еще раз может утвердить нас в идее о случайности изменений фондового индекса DJI.
4. Рассмотрим внутридневную разницу между максимальными и минимальными значениями фондового индекса DJI за период с октября 1928г. по октябрь 1999г. (17838 дней, в процентах по модулю). Это даст нам возможность узнать об обычном размахе движений фондового индекса в ходе одной торговой сессии. Графически разница между внутридневными максимальными и минимальными значениями фондового индекса DJI выглядит следующим образом.
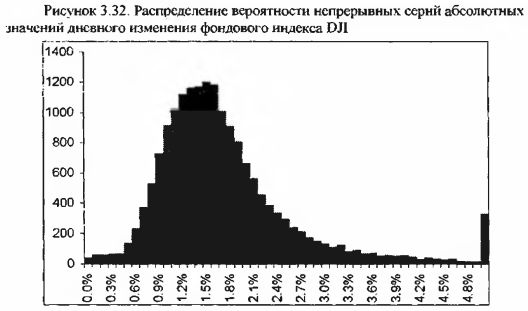
Плотность вероятности внутридневной разницы выглядит идентично почти идеальному логнормальному распределению. Однако данный ряд не является логнормальным. Здесь мы видим типичный пример левостороннего смещения, обусловленного процентным характером переменной.
Можно провести левостороннюю и правостороннюю проверку, те. определить уровни значимости с обеих сторон для трех интервалов 0 1%, 1% и 5%. При левосторонней проверке определяется вероятность того, что размах окажется меньше уровня значимости. Правосторонняя поверка дает вероятностную оценку того, что размах окажется выше уровня значимости.
На основании эмпирических данных можно составить следующую таблицу:

Из этой таблицы видно, что реально значимым уровнем может быть только 5%-ный уровень, так как остальные настолько незначительны, что вряд ли получится использовать их в работе.
|



















