|
«Высшая ловкость состоит в том, чтобы всему дать истинную цену»
Франсуа де Ларошфуко, французский писатель
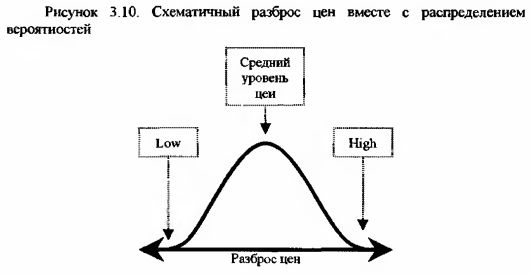
Так как одна цена, даже средняя и определенная самым лучшим способом все равно является достаточно условной величиной, то более оправданно говорить об интервале цен, отражающих инвестиционные предпочтения активных участников рынка. С точки зрения теории вероятностей интервал дает границы для нахождения наиболее вероятного диапазона цен, а средняя – центр интервала.


Со статистической точки зрения можно также говорить о том, что интервалы дают приближенную оценку уровней поддержки и сопротивления, значимость которых мы рассмотрели в предыдущем пункте.
Существует несколько разновидностей статистических показателей вариации (разброса, рассеяния), которые задают интервал наиболее вероятного диапазона исследуемых значений. Здесь мы рассмотрим самые распространенные среди них:
- стандартное отклонение;
- дисперсию.
Обыденный физический смысл показателей вариации основывается на двух постулатах.
Во-первых, мир вокруг нас не является черно-белым. Существует множество оттенков и красок, различных переходных состояний в любом процессе. На финансовых рынках это буйство красок проявляется в широких диапазонах колебания цен.

Во-вторых, явления редко находятся в крайних состояниях, обычно протекая у неких средних зон. Для финансовых рынков это находит свое отражение в том, что цены имеют тенденцию колебаться не у крайних своих значений – high и low, а возле средних уровней.
Стандартное отклонение (называемое также среднеквадратичным отклонением) – статистическая мера вариации (разброса) переменных X вокруг среднего значения. Обозначается с и рассчитывается по следующей формуле:
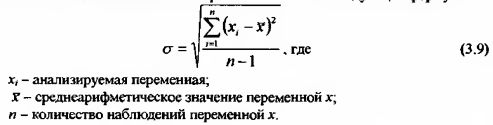
Дисперсия является еще одним показателем вариации и обычно обозначается как DX. Рассчитывается дисперсия как возведенное в квадрат стандартное отклонение:
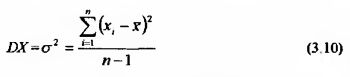
Дисперсию обычно используют при оценке риска, а стандартное отклонение – при оценке волатильности, что очень важно при работе с опционами.
Например.
Необходимо найти стандартное отклонение ряда значений индекса Dow Jones Industrial (DJI, close) за январь 1999 года.
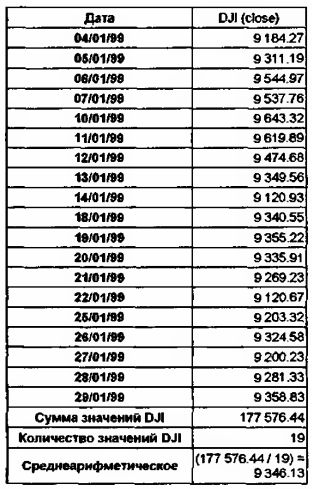
Количество наблюдений индекса DJI за этот период составляет 19 (п = 19).
Среднеарифметическое значений индекса DJI за этот период составило 9346.13 (х = 9346.13).
Для вычисления стандартного отклонения значений индекса DJI от среднеарифметического значения необходимо выполнить следующие действия.
1. Рассчитать разницу между конкретными i-тыми значениями индекса DJI и среднеарифметическим значением:
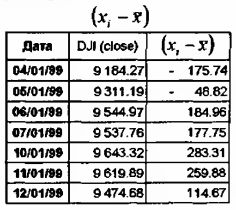
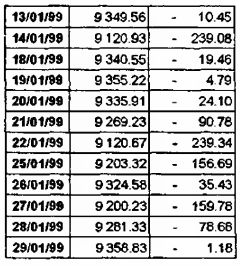
2. Возвести рассчитанную согласно п. 1. разницу в квадрат:
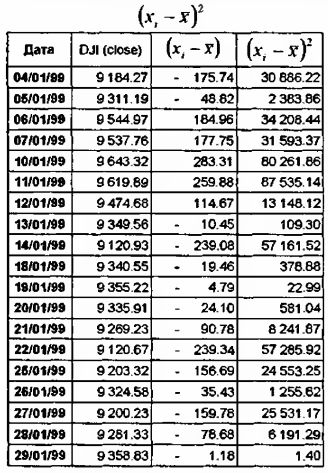
3. Просуммировать все полученные согласно п.2. значения:
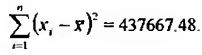
4. Разделить полученное согласно п.3. значение на n (n = 19):
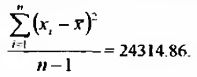
5. Извлечь из полученного согласно п.4. значения квадратный корень:
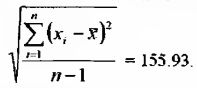
Это значение и будет являться искомым стандартным отклонением σ.
Здесь же следует отметить, что правильнее определять стандартное отклонение большинства финансовых показателей, особенно таких как фондовые индексы, исследуя не их абсолютные значения, а обрабатывая относительные изменения (в процентах к предыдущему значению). Например, 100 пунктов изменения DJI в декабре 1998 года очень сильно отличаются от тех же 100 ПУНКТОВ изменения DJI в августе 1999 года. В декабре такое изменение соответствовало почти 1.1%, а в октябре, всего через семь месяцев – 0.9%.
Когда необходимо найти стандартное отклонение не конкретных значений ряда, а интервалов этих значений или же есть возможность оперировать средневзвешенными значениями, используется несколько видоизмененная формула:
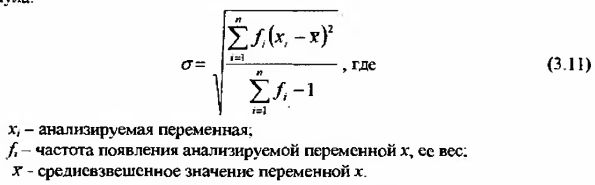
Например. Возьмем ряд котировок спроса (bid) валютного соотношения GBP/USD за один день 26 июня 1997 года, сгруппированных в диапазонах по 5 ПУНКТОВ:
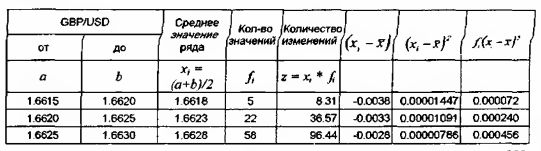
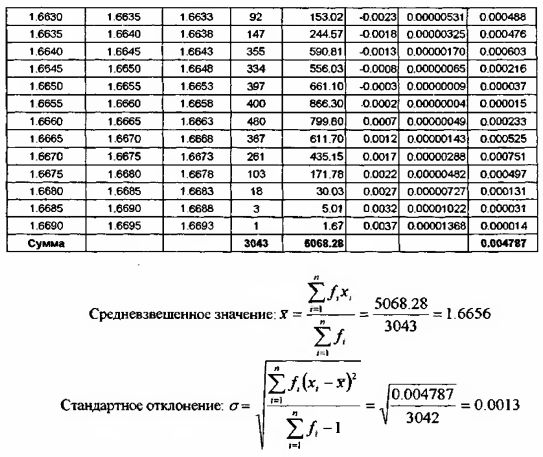
Это означает, что котировки спроса GBP/USD 26 июня 1997 года в основном находились в пределах 1.6656 ± 0.0013, т.е. в пределах от 1.6643 до 1.6669.
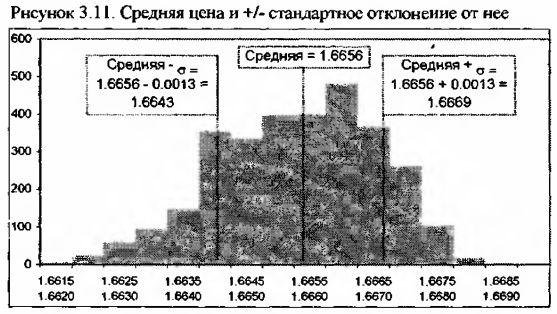
Рассматривая стандартное отклонение, нельзя не обойти вниманием следующее значимое понятие из области статистического исследования финансовых рынков – распределение, которое также является одним из ключевых моментов теории вероятностей.
Распределением называют вероятность принятия случайной величиной какого-либо конкретного значения.
В результате исследования любого статистического ряда можно составить функцию распределения, которую иногда также называют плотностью вероятности.
Выделяют несколько основных типов распределений:
- нормальное распределение;
- логнормальное распределение;
- биноминальное распределение;
- распределение Пуассона.
Нормальное и логнормальное распределения являются непрерывными распределениями, а биноминальное и Пуассона – дискретными распределениями. Главное отличие между непрерывными и дискретными распределениями заключается в характере исследуемых рядов. Так, непрерывными величинами можно признать процентные изменения цен, а дискретными – собственно цены. Если первые зачастую только после округления приводятся к целым значениям, то последние обычно изначально являются целыми, также как и большинство предметов в природе.
Результатом построения и анализа любого типа распределения будет вероятностная оценка наступления конкретного события или ряда событий.
Наиболее известным и, наверное, наиболее распространенным в практической деятельности является нормальное распределение, иногда называемое распределением Гаусса. Данный вид распределения часто встречается в природе. Например, закону нормального распределения подчиняется случайная выборка людей по росту, весу и даже интеллектуальному развитию. Выглядит нормальное распределение как симметричная колоколообразная кривая. Среднеарифметическая ряда, подчиняющегося закону нормального распределения, равна моде и медиане этого ряда.
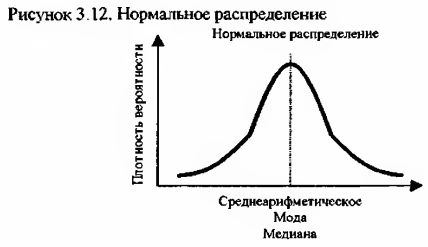
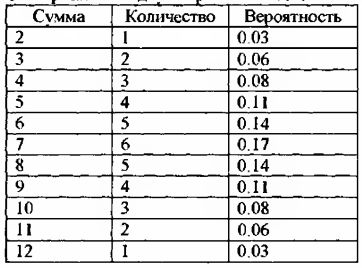
Если мы рассмотрим очень большое количество одновременных бросков двух игральных костей и накопим статистический ряд сумм этих костей, то значения в нем будут максимально приближены к нормально распределенным. Так как вероятность выпадения каждой отдельной грани игральной кости одинакова и равна приблизительно 0.167 (1/6), то, казалось бы, вероятность суммы двух игральных костей также равновероятна. Однако это не так. Составим таблицу всех возможных исходов одновременного выбрасывания двух игральных костей.
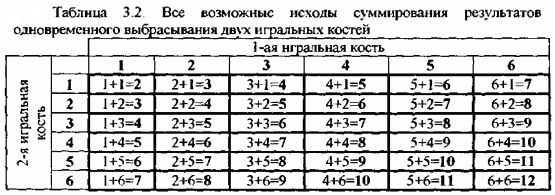
Как мы видим, всего может быть 11 исходов этих сумм: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и 12. Если же мы составим таблицу распределения вероятности образования тех или иных сумм, то картина получится далекая от той, которую можно было бы предположить заранее.
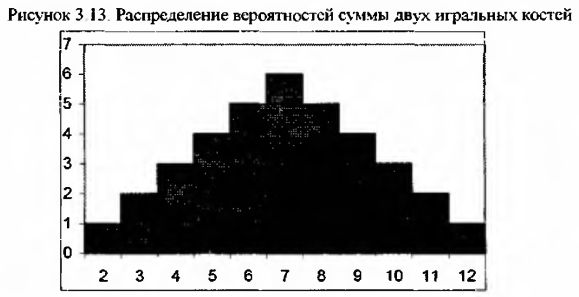
На следующем рисунке мы видим, что суммы двух игральных костей подчиняются закону нормального распределения.
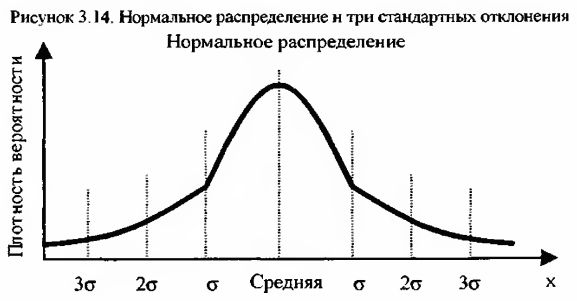
Если исследуемый ряд подчиняется закону нормального распределения, то большая часть всех значений этого ряда, а точнее в среднем 68.27% будут находиться в интервале плюс-минус стандартное отклонение от среднеарифметической. Еще большая значимость стандартного отклонения при рассмотрении нормальных распределений в том, что в среднем 95.45% всех значений находятся в интервале плюс-минус два стандартных отклонения, а 99.73% в интервале три стандартных отклонения от среднеарифметической. Таким образом, зная величину стандартного отклонения, можно с достаточно высокой степенью достоверности – вероятность 99.73% – определить, что некая искомая величина будет находиться в определенном интервале.
Формула для вычисления функции нормальной плотности вероятности наступления конкретного события для ряда, подчиняющегося закону нормального распределения выглядит следующим образом:

Для определения вероятности наступления события x достаточно подставить значение этого х в формулу (3.12) и получить искомое значение.
Например.
Одновременно и независимо друг от друга выбрасывается две игральных кости и производится суммирование выпавших на них чисел. Найдем вероятность получения суммы в 5 единиц.
1. Сначала необходимо определить среднеарифметическое значение всех возможных вариантов сумм отдельных граней двух кубиков для чего составим следующую таблицу.
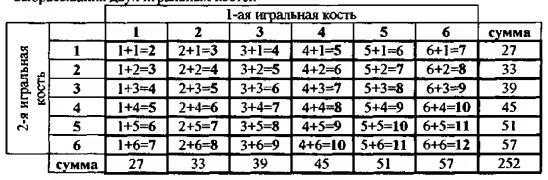
Сумма всех возможных вариантов = 252.
Всего вариантов = 36.
Среднеарифметическое значение одного варианта (а) = 252/36 = 7.
2. Следующим действием необходимо определить стандартное отклонение имеющегося ряда.
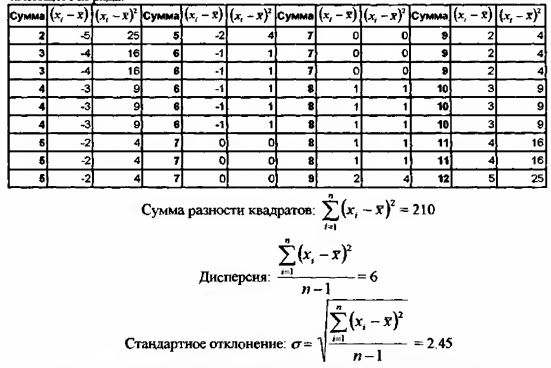
3. Рассчитаем значение вероятности для конкретного значения х = 5:
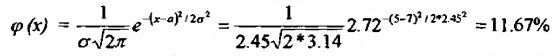
Это значение вероятности немного отличается от действительной вероятностной оценки (11.11%), что объясняется дискретным характером исследуемого ряда. На приведенном ниже рисунке видны различия между распределением вероятности по нормальному закону и действительной плотностью вероятностей.
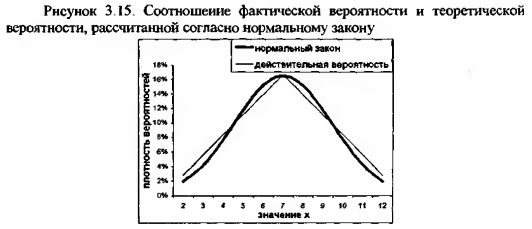
Сглаженный характер функции нормальной плотности значении х подтверждает обоснованность применения этого вида распределения для непрерывных рядов. Однако вместе с тем видно, что достаточно высокая достоверность полученной оценки вероятности позволяет использовать нормальное распределение и для дискретных длинных рядов.
Когда требуется определить вероятность того, что х будет находиться в некоем значимом интервале, что является гораздо более обычным для применения финансовой статистики по сравнению с оценкой вероятности наступления единичного х, использование формулы (3.12) будет затруднено. Обычно в этих случаях используют следующую упрошенную формулу:
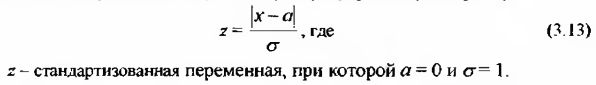
Графически величина z выглядит как площадь под функцией нормального распределения от z до бесконечности: заштрихованная область после z (при z > а).
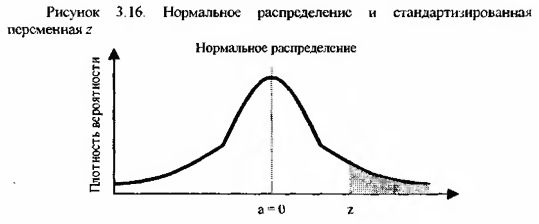
При помощи статистической таблицы «Стандартное нормальное распределение» (дана в приложении) значение z дает искомую интервальную вероятность. Если z = а, то z = 0, а вероятность такого интервала равна 50%.
Например.
Рассмотрим ряд изменений фондового индекса DJI за период с 04 января 1915г. по 27 августа 1999 года. Здесь нам придется сделать предположение, что данный ряд подчиняется закону нормального распределения. Впрочем, если это не так. то плотность вероятности этого ряда даже близко не будет напоминать нормальное распределение. На приведенном ниже рисунке видно, что ряд изменений индекса DJI очень похож на нормальное распределение, поэтому мы будем исходить из закона нормального распределения.
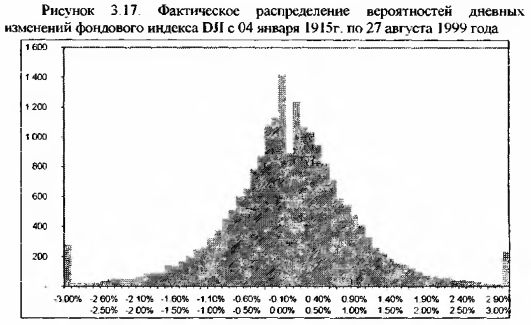
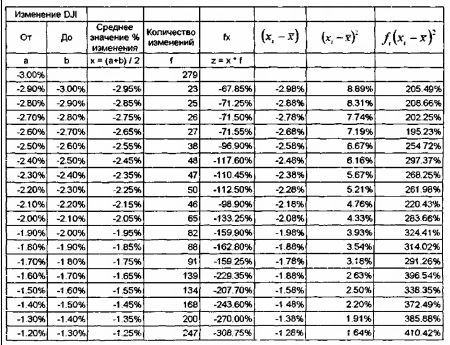
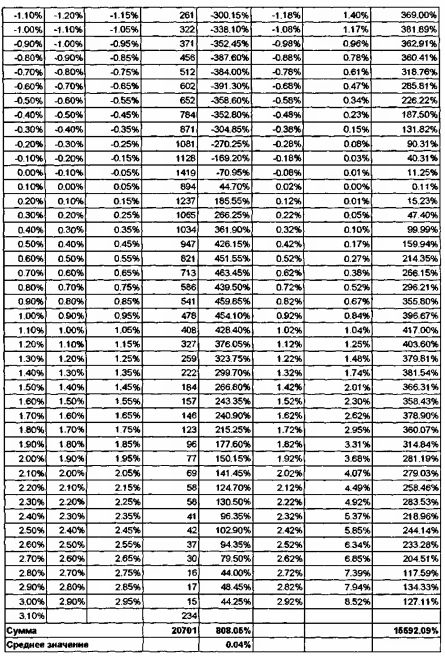
Найдем вероятность роста фондового индекса DJI на 1% и более, для чего в том числе необходимо рассчитать среднеарифметическое значение данного ряда и стандартное отклонение. Так как ряд интервальный, то для расчета стандартного отклонения применим формулу (3.11).

Зная среднеарифметическое и стандартное отклонения ряда можно определить искомую вероятность роста фондового индекса DJI на 1% и более.
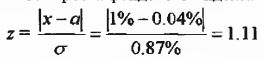
По таблице находим значение вероятности, соответствующее полученной величине z: 0.1335 или 13.35%.
Если сравнить это значение вероятности с фактической вероятностью данного события, полученной на основании эмпирических данных суммарной вероятности за прошлый период (12.33%), то видно достаточно точное соответствие этих величин.
Используя z можно получать доверительные пределы. Последние определяют верхнюю и нижнюю границу интервала от среднеарифметического значения ряда, в котором находится необходимое количество значений ряда. Доверительные пределы используются, кода есть величина необходимой вероятности, но неизвестно значение интервала, при котором возможно получить эту вероятность.
Например.
Для приведенной выше совокупности значений изменений фондового индекса DJI необходимо найти те крайние границы интервала, с тем, чтобы в него поместилось 90% всех значений ряда.
Из таблицы «Стандартное нормальное распределение» найдем то значение r, при котором вероятность равна 0.05 ((1-0.90)/2). Оно находится в интервале от 1.64 до 1.65. Возьмем за среднее 1.645.
Подставив это значение z в формулу (3.13) получим следующее уравнение:
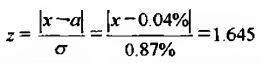
В этом уравнении неизвестным является только искомый х. После перестановки и выделения х получаем: х = 1.645 * 0.87% + 0.04% = 1.47%.
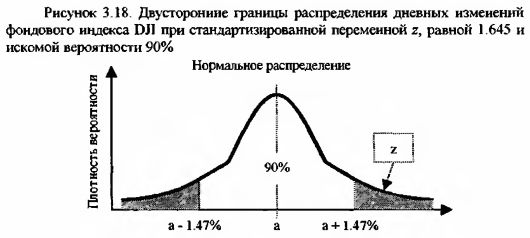
Можно также определить более сложную интервальную вероятность, в которой обе границы оцениваемого интервала задаются.
Например Определим вероятность того, что фондовый индекс DJI окажется в интервале от -0.5% до +1%.
Для этого рассчитываются два значения z.
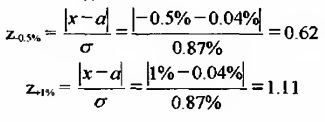
Значение вероятности для z-05% – 0.2676, а для z+1%- 0.1335.
Искомая вероятность определяется путем вычитания этих двух значений
из 1:
Р = 1 – (0.2676 + 0.1335) = 0.5989 или 59.89%
Таким образом, вероятность того, что фондовый индекс DJI окажется в интервале от -0.5% до +1% составляет 59.89%.
Логнормальное распределение
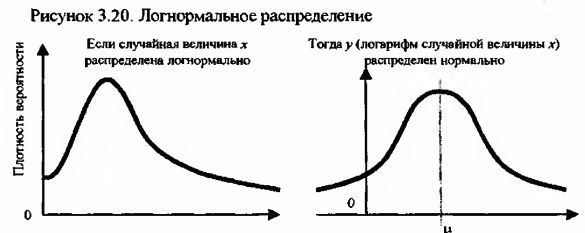
Нормальное распределение может принимать отрицательные значения, что для финансовых рынков неприемлемо, ведь ценные бумаги, валюты и другие активы не могут стоить меньше ноля. Этого недостатка лишено логнормальное распределение. Оно, в силу специфики расчета, не может быть отрицательным.
Построение логнормального распределения исходит из того, что случайные величины подчиняются закону нормального распределения. Этот факт доказывается центральной предельной теоремой. Согласно этой теореме математическое ожидание большого числа независимых выборок будет нормально распределено вне зависимости от действительного распределения данных при условии конечной дисперсии. Это утверждение имеет самое непосредственное отношение к финансовым рынкам.
Например. Если рассмотреть потиковое изменение индекса DJI, то мы можем ожидать только три исхода – индекс вырастет (обозначим как +1), упадет (-1) или останется без изменений (0). Предположим, что эти исходы равновероятны и вероятность каждого из них равна 33.33%.

Дальше, при следующем изменении индекса DJI он снова может вырасти, упасть или остаться без изменений. Суммарный исход двух тиковых изменений будет выглядеть следующим образом:
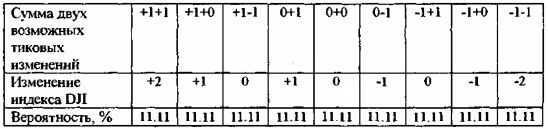
Отсюда мы видим, что всего исходов суммарного двухтикового изменения индекса DJI может быть пять: +2, +1, 0, -1, -2. Распределение вероятности этих изменений выглядит следующим образом (просуммируем вероятности всех однотипных исходов):

После следующего, третьего тикового изменения возможных исходов становится уже семь, а распределение вероятности приобретает следующий вид:

Как видно, чем дальше мы рассматриваем потиковые изменения индекса DJI, тем меньше становится вероятность крайних значений. При этом также очевидно, что распределение вероятности с каждым добавлением нового тика принимает все более колоколообразную форму нормального распределения.
Здесь мы применяли правило сложения изменений: +1+1-1, +1-1+0 и т.д. Однако при работе с процентными числами и вообще реальными числами изменений того же индекса DJI этот подход никак нельзя назвать правильным.
Например. Как мы знаем, за одно тиковое изменение индекс DJI может измениться на произвольную величину, например, на +0.2 пункта и на +20 пунктов. И первый, и второй случай являются положительным результатом которому мы присвоим ранг +1. Однако в процентном соотношении эти плюсы далеко не одинаковые и было бы по меньшей мере не логично говорить об их равенстве. Еще большие проблемы возникают, когда первое изменение индекса DJI происходит на +0.2 пункта, а второе на -20. Одинаковый ранг этих изменений (+1 и -1 соответственно) в этом случае введет нас в заблуждение относительно происходящего на рынке, ведь суммарное изменение индекса DJI было на самом деле не 0 (+1 – 1 = 0), а – 19.8 (+0.2 – 20 = -19.8).
Для точного отображения происходящего для этих чисел применяют правило умножения.
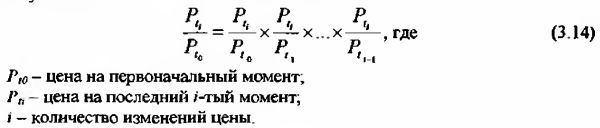
Применив к формуле (3.14) логарифмирование получим:
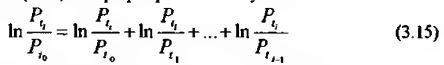
Если мы предположим, что каждая цена Рt является случайной и независимой величиной, подчиняющейся закону нормального распределения, то соотношение 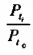 также является случайной величиной. Таким образом, согласно центральной предельной теоремы сумма натуральных логарифмов также является случайной величиной. Таким образом, согласно центральной предельной теоремы сумма натуральных логарифмов 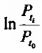 будет являться нормальной распределенной. Именно этот факт и используется исследователями при построении логарифмически нормального распределения. будет являться нормальной распределенной. Именно этот факт и используется исследователями при построении логарифмически нормального распределения.
Вторым отправным моментом, почему при работе на финансовых рынках эффективнее использовать не нормальное, а логнормальное распределение, является некорректность сложения процентов.
Например, если вы при инвестировании 100 единиц сначала получите доход в размере 10%, а затем убыток 10%, то это не означает, что в результате этих движений вы остались при своих. И действительно. Рост стоимости актива на 10% сопровождается абсолютным ее увеличением на 10 единиц – со 100 до 110. Последующее падение стоимости актива на 10% сопровождается абсолютным ее уменьшением на 11 (!) единиц – со 110 до 99. Для корректного исчисления процентных изменений обычно применяют правило не сложения процентов, а умножения.
Так, умножение 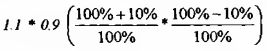 дает правильное значение 0.99. дает правильное значение 0.99.
Другим способом, позволяющим правильно оценить процентное изменение, является логарифмирование. В принципе, могут применяться логарифмы с разными основаниями, но обычно в финансовой статистике используют натуральные логарифмы. В нашем примере итоговую доходность можно было определить следующим способом:
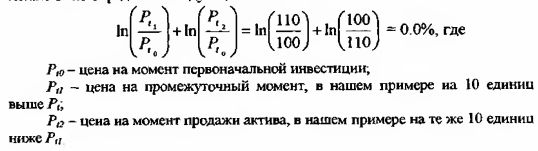
Таким образом, и цена никуда не сходила, и доходность составила 0%, что полностью соответствует истине.
При обычном способе определения доходности имеем:
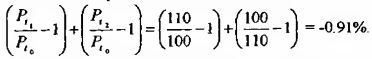
Здесь цена, как и в предыдущем расчете, никуда не сходила, а убыток возник. «Источником» убытков является, как вы уже поняли, неправильность примененной формулы. Дело здесь в том, что проценты изменяются с разной скоростью в зависимости от абсолютных изменений переменной: как мы уже могли заметить, рост переменной сопровождается более значительным увеличением процентов по сравнению с уменьшением переменной.
Приведенными выше расчетами и примерами показываются преимущества логнормального распределения по сравнению с нормальным применительно к процентным данным.
Мода, медиана и среднеарифметическая логнормального распределения не совпадают.
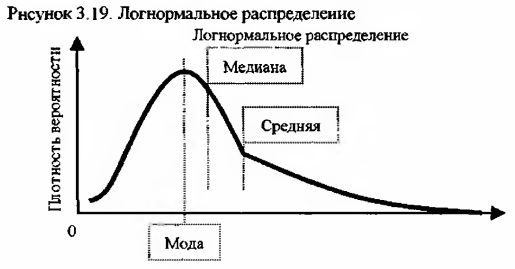
Левостороннее смещение моды и медианы в логнормальном распределении объясняется тем, что процентное изменение значений в ряде неадекватно абсолютному изменению этих значений. Согласно вышеприведенного примера падение доходности на 10% и ее рост на те же 10% будет отражены в цене как падение на 9.52 и рост на 10.52 соответственно. С увеличением процентов разница в абсолютных значениях становится еще более существенной.
Математическое ожидание, дисперсия и стандартное отклонение случайной величины х, подчиняющейся закону логнормального распределения, вычисляется по следующей формуле:

Логнормальное распределение, как правило, используется при оценке опционов и расчете доходности портфельных стратегий.
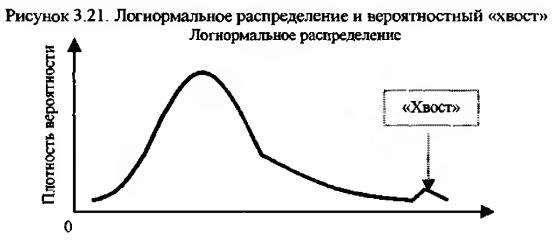
Так как на практике длина любого ряда наблюдений не признается бесконечной, то можно обнаружить одно отклонение теоретического логнормального распределения от эмпирического. Это отклонение заключается в том, что «хвост» распределения, который теория зачастую отбрасывает как маловероятный и незначительный, в результате суммирования бесконечно далеких значений накапливает достаточно существенную вероятность. На практике рынок оценивает вероятность появления правого оконечного, граничного значения в логнормальном распределении значительно выше, чем это предписывается теорией. Данный факт с успехом можно применять при работе с опционами, которые находятся далеко «вне денег» и которые при их оценке значительно недооценены.
Распределение Пуассона
Когда известно среднеарифметическое значение события, чью вероятность необходимо определить, число j достаточно велико, а количество попыток к незначительно используется распределение Пуассона, которое описывается следующим образом:
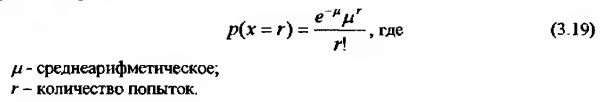
Например. Вычислим вероятность того, что в течение ближайшего месяца фондовый индекс DJI по итогам дневной торговой сессии дважды резко упадет. Величину падения определим в 2% и более. Анализируя прошлые движения индекса DJI за период с 1915 по 1999 годы (1016 месяцев) можно отметить, что за это время всего произошло 617 падений на 2% и более. Таким образом, среднее число падений индекса DJI на 2% и более в среднем за одни месяц составляет 0.61.
Вероятность того, что в течение следующего месяца по крайней мере дважды по итогам дневной торговой сессии мы сможем наблюдать сильное падение фондового индекса DJI будет составлять:
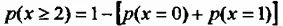
Для этого необходимо будет рассчитать отдельно вероятности одного и нулевого случая падения на 2% и более:
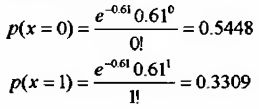
Тогда,
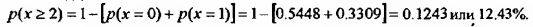
Биноминальное распределение
Биноминальное распределение является одним из наиболее интересных и важнейших распределений дискретных чисел. Дискретными называют те числа, которые могут принимать конечное, счетное количество значений.
Биноминальные распределения, как следует из самого названия, состоят из переменных, которые могут принимать только два значения в один момент времени и наступления события. Например, 0 или 1; "прибыль" или "убытки"; "угадал" или "не угадал"; "купил" или "продал"; "рост" или "падение" и т.д.
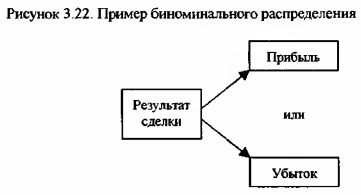
Второе обязательное условие для построения биноминального распределения – все события внутри одного эксперимента и эксперименты между собой должны быть независимы.
Третье условие – вероятность наступления одинаковых событий в каждом последовательном эксперименте (пробе) должна быть равна. При этом вероятность одного события внутри одного эксперимента может отличаться от вероятности наступления другого события.
Четвертое, и последнее, обязательное условие построения биноминального распределения – фиксированная длила ряда в каждом эксперименте (пробе).
Например. Предположим, что вы совершаете сделки с фьючерсными контрактами, а результаты этих сделок являются случайными и независимыми друг от друга, а вероятность каждого варианта результата равновероятна. Всего возможны три варианта последующего результата сделки: доход (+1), убыток (-1) и нулевой результат (-1). Нулевой результат признается убыточным, так как спрэд, комиссия и другие расходы, связанные со сделкой, оказывают негативное влияние на финансовый результат. Таким образом, вероятность положительного результата равна 33.33, а отрицательного – 66.67. Построим "дерево" биноминального распределения финансовых результатов для четырех подряд сделок.

Для определения вероятности успеха при биноминальном распределении необходимо сначала рассчитать число комбинаций исходов j в выборке из и вариантов по следующей формуле:
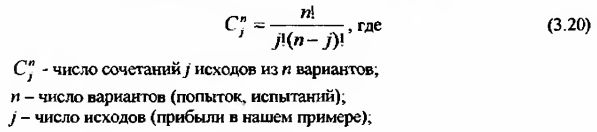
Зная количество успешных попыток можно рассчитать их вероятность:
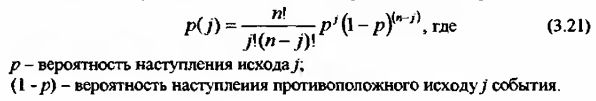
Например. Рассчитаем вероятность того, что 4 из 6 сделок у нас будут прибыльными, если вероятность успешной, прибыльной сделки составляет 33.33%.
Количество успешных попыток:
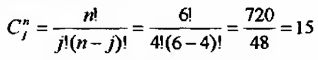
Вероятность достижения искомого результата:
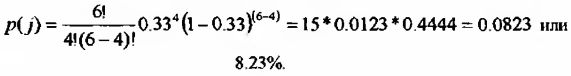
Триноминалъное распределение
Триноминалъное распределение является эквивалентом биноминального распределения. Здесь, в отличие от биноминального распределения, допускается три возможных варианта событий в результате каждого испытания.
Триноминалъное распределение позволяет рассчитывать вероятность сложных цепочек и комбинаций событий, каждое из которых может принимать три разных вида (исхода).
Например, построим триноминальную модель изменения фондового индекса DJI по итогам дневной торговой сессии. Существует три возможных варианта изменения индекса: рост более чем на 0.5% (+1), падение более чем на 0.5% (-1) и стабильность в диапазоне от -0 5% до +0.5% (0). Вероятность наступления этих вариантов признается равной соответственно 23.56%, 27.13% и 49.31%, что подтверждается эмпирическими данными, рассчитанными ранее.
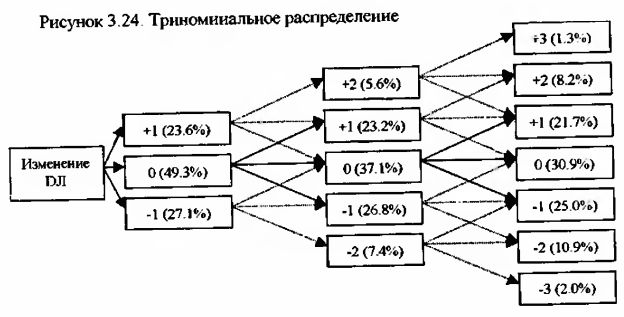
Для определения вероятности успеха при триноминальном распределении необходимо сначала рассчитать количество комбинаций всех возможных вариантов по следующей формуле:

Зная количество комбинаций всех возможных вариантов можно рассчитать вероятность искомого варианта:
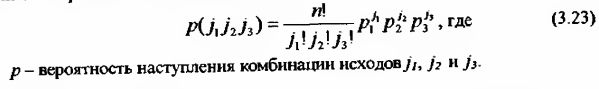
Например. Определим вероятность того, что в течение ближайших 10 торговых сессий мы будем наблюдать 5 растущих дней (рост более чем на 0.5%), 4 стабильных дня (стабильность DJI в диапазоне от -0.5% до +0.5%) и только один падающий день. Как мы уже помним, вероятности наступления этих вариантов равны соответственно 23.56%, 49.31% и 27.13%.
Тогда:
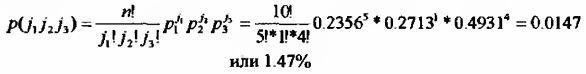
|



















