|
Работа на финансовых рынках предполагает вероятностную оценку будущих событий. Происходит это в первую очередь из-за недостатка информации, зачастую испытываемого людьми, проводящими анализ и принимающими решения. О свойствах информационного «голода» мы поговорим в главе, посвященной психологии, а здесь остановимся на математическом описании этого процесса. Главным здесь является наше практически полное незнание будущего, которое и является объектом торговли на финансовых рынках. Так, покупая фьючерсный контракт, мы рассчитываем на рост стоимости товара, на который выписан фьючерс. Если при этом вы уверены в том, что поступаете правильно на все 100 процентов, то это не больше чем ложная самоуверенность. К сожалению, на рынке нельзя быть ни в чем уверенным. Однако человек не только не знает будущего, но зачастую имеет очень плохую и недостоверную информацию о прошлом. Только близкое прошлое доступно человеку для максимально возможной полноты информации, дальнее же закрыто за завесой тайны не хуже будущего. Более-менее человек разбирается в настоящем. Однако и здесь обилие информации не дает основания утверждать, что человек знает окружающее его настоящее. Таким образом, куда ни кинь взгляд – в прошлое, настоящее или будущее – человек везде ограничен тем объемом информации, который он может воспринять и проанализировать, а также к которому он имеет доступ. Все остальное относится к области неизвестного, а неизвестное, как мы знаем, и пугает и притягивает людей. Отсюда появляются легенды и гипотезы о рынке – то он случайный, то эффективный, то хаотичный и т.д. В этом мы напоминаем пещерных людей, пытающихся объяснить природные явления (например, такие как гром или молния) доступными соответствующему уровню знаний и, соответственно, накопленной информации об окружающем мире, понятиями.


По причине постоянного недостатка информации нам только и остается говорить о вероятности наступления того или иного события. Я не утверждаю, что движение цен на рынке – это абсолютно случайное явление, хотя именно случайные события являются объектом изучения теории вероятностей.
Случайные события
Случайное событие – событие, которое в зависимости от исхода опыта (случая) принимает различные значения и которое невозможно точно предсказать.
Как мы знаем, абсолютно стопроцентное предсказание динамики цен в течение сколько-нибудь продолжительного периода времени до сих пор является нерешенной задачей. Происходит ли это по причине несовершенства нашего понимания или недостатка информации, факт остается фактом -поведение рынка остается непредсказуемым. Непредсказуемостью обладают и случайные события. Именно эта схожесть используется теорией случайных блужданий (random-walk theory) в качестве обоснования своего существования.
Здесь следует провести краткий обзор господствующих теорий, лежащих в основе большинства современных финансовых решений. К ним можно отнести теории:
- рыночного равновесия;
- эффективного рынка;
- случайных блужданий;
- игр.
Теория рыночного равновесия исходит из постулата о том, что рынок стремится к равновесному состоянию между спросом и предложением. Данная теория не исключает отклонений от равновесного состояния.
Согласно теории эффективного рынка вся новая информация практически моментально закладывается в рыночные цены. Таким образом, нельзя получить прибыль, ориентируясь на какую-либо информацию или же на прошлую динамику цен. Выводы теории эффективного рынка:
- никто не может прогнозировать динамику рыночных цен;
- все рыночные цены являются справедливыми для данных активов, а неверно оцененных товаров нет.
Против теории эффективного рынка говорит практика финансовых рынков. Во-первых, информация разными людьми воспринимается по-разному, о чем мы уже говорили в главе, посвященной психологии. Во-вторых, где гарантия того, что полученная рынком информация является истинной, а не ложной. В-третьих, в разные моменты времени одна и та же информация может трактоваться по-разному. В-четвертых, очень маловероятно чтобы рыночная цена в каждый момент времени являлась справедливой или истинной. Здесь скорее можно поверить в то, что рыночная цена периодически пересекает справедливую цену, переходя из состояния завышенной в состояние заниженной по отношению к ней цены, и наоборот.
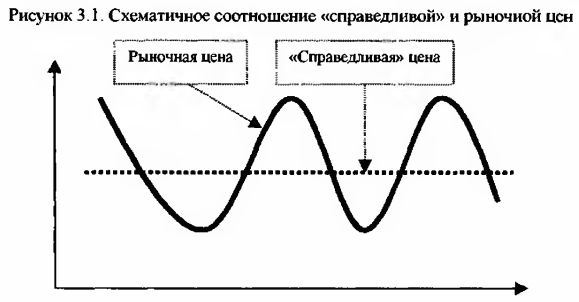
Теория случайных блужданий продолжает теоретические измышления апологетов теории эффективного рынка. В теории случайных блужданий информация подразделяется на две категории – предсказуемую, известную и новую, неожиданную. Если предсказуемая, а тем более уже известная информация уже заложена в рыночные цены, то новая неожиданная информация в цене пока еще не присутствует. Одним из свойств непредсказуемой информации является ее случайность и, соответственно, случайность последующего изменения цены. Теория эффективного рынка объясняет изменение цен поступлениями новой неожиданной информации, а теория случайных блужданий дополняет это мнением о случайности изменения цен.
Краткий практический вывод теории случайных блужданий – игрокам рекомендуется использовать в своей работе стратегию «покупай и держи». Следует заметить, что расцвет теории случайных блужданий пришелся на 70-е годы, когда на фондовом рынке США, традиционно являющемся главным полигоном проверки и использования всех новых теорий, не было явных тенденций, а сам рынок находился в достаточно узком коридоре.
Против теории случайных блужданий можно привести следующие доводы. Во-первых, если в какой-либо момент времени можно быть готовым к появлению неожиданной информации и иметь готовые сценарии реагирования на нее, то она становится не такой уж неожиданной. Во-вторых, несмотря на внешнюю схожесть кривой случайных блужданий и графиков рыночных цен никто еще не доказал, что рынок есть событие абсолютно непредсказуемое (впрочем как не доказано и обратное). По крайней мере, среди математиков есть мнение, что рынок – это не абсолютно случайное явление, так как на нем появляются законы психологии. В третьих, никто еще не отменял экономических законов и устоявшихся экономических закономерностей.
Как пишет Джон Дж.Мерфи,
«... чаще всего случайность определяется неспособностью установить систематические модели ила закономерности в динамике цен»
В результате этого отрицания данная теория не рекомендует заниматься поисками тенденций. Технический анализ, речь о котором пойдет позже в одной из глав, использует в своей базе именно знание тенденций. Поэтому его смело можно отнести к прямой противоположности теории случайных блужданий. Здесь, однако, следует отметить, что осцилляторная часть технического анализа в своей основе также использует подходы теории случайных блужданий, хотя классический технических анализ и приспособил осцилляторы для анализа трендов.
Теория игр наиболее близка к вероятностным процессам. По этой причине мы уделим ей повышенное внимание.
В теории игр исследуются ситуации с двумя или более участниками, интересы которых полностью или частично противоречат друг другу. Предметом изучения этой теории является анализ и прогноз действий разных игроков, направленных на достижение одной цели (захват рынка, максимизация прибыли и т.п.).
Применительно к динамике цен действия одного игрока по изменению цены могут привести к действиям по изменению цены другим игроком. Тем самым само изменение цены является информацией для рынка, причем иногда гораздо более важной, нежели какие-либо фундаментальные новости. Об этом красноречиво свидетельствуют резкие всплески цен при проходе ключевых уровней сопротивления и поддержки, когда, кроме самого факта изменения цены на рынке ничего не происходит.
Теория игр помогает игрокам правильно построить собственную стратегию, реализуя которую можно не только приспособиться к действиям других рыночных участников, но и максимизировать искомый результат. Выбирая стратегию, игрок должен учитывать возможные ответные шаги других игроков. При этом предполагается, что все игроки выбирают наилучшие стратегии и тактические шаги, хотя, по-моему, это далеко от истины.
Наиболее простым и распространенным отражением игры является построение матрицы результатов. Каждый элемент этой матрицы показывает результат, ожидаемый конкретным игроком для любой возможной стратегии. Здесь стоит отмстить, что игроком в целях теории игр признается только активный участник, который может влиять на ситуацию и действия других игроков. Пассивные участники, которые только следуют за рынком, игроками, при всем их желании, называться не могут.
Например. В представленной ниже матрице результатов показаны результаты игрока А в игре с нулевой суммой для двух участников:

Здесь, если игрок А выбирает стратегию а3, а игрок В стратегию b2, то результат для игрока А составит -10, а для игрока В +10. Задача каждого игрока состоит в том, чтобы выбрать стратегию, максимизирующую искомым результат, учитывая стратегию другого игрока. Так, с точки зрения игрока А наилучшие реакции на три возможных стратегии игрока В составляет следующие пары: (b1, а3), (b2, а1), (b3, a2). Для игрока В наилучшие реакции на три возможных стратегии игрока А составляют следующие пары: (a1, b3), (a2, b3), (а3, b2). Единственной пересекающейся стратегией здесь является пара (а2, b3), которая присутствует в наилучших реакциях обоих игроков. Таким образом, одновременный выбор 2-й и 3-й стратегий игроков А и В соответственно и будут являться решением настоящей матрицы результатов. Однако жизненная практика показывает, что не все так просто. Во-первых, игроки могут и не догадываться о наилучшем выборе, принимая решения на основании других решающих правил. Во-вторых, действия игроков очень редко бывают одновременными, что дает одному из игроков преимущество. В-третьих, стратегий может быть неисчислимое множество. В-четвертых, в жизни матрицы результатов являются динамическими системами, в отличие от представленного выше статического примера.
Тем не менее, маркетмейкеры (в широком понимании этого слова) практически постоянно вынуждены соизмерять свои действия с поведением, как действительным, так и возможным, других участников, в том числе рыночной массой в целом.
Главной проблемой выбора наилучшей стратегии игры является недостаток и неопределенность информации. Это предопределяет необходимость использования вероятностных методов в ходе решения матрицы.
К теории игр можно подойти также с той точки зрения, что рынок представляет собой сообщество игроков, в котором могут договориться только крупные игроки. Соответственно, только они могут получить выгоду от сотрудничества и максимизировать свои доходы. Все остальные вынуждены действовать строго в одиночку и соперничать друг с другом и с крупными игроками. Согласно теории игроки, не сотрудничающие между собой, неизбежно будут от соперничества терять. Это означает, что мелкие игроки получают выигрыш, только когда крупные игроки с ними делятся.
Подход теории игр мне кажется более обоснованным для применения на финансовых рынках по сравнению с теорией случайных блужданий Причиной этого является, с моей точки зрения то, что все последующие числа закономерных рядов порождены предыдущими, что и кто бы ни пытались оказать на них влияние
Теория вероятностей
Все сказанное в предыдущем пункте дает нам основание относиться к рыночным явлениям как к случайным и, соответственно, применять теорию вероятностей Таким образом, без понимания теории вероятностей предпринимать последующие шаги вряд ли имеет смысл.
Вероятность представляет собой количественную меру того, что какое-либо случайное событие произойдет. Вероятность может принимать значение в промежутке от 0 (невозможное событие) до 1 (событие, которое обязательно наступит). Иногда вероятность описывают в процентах. В этом случае границы значения вероятностей будут составлять 0% и 100% соответственно.
Классическая формула для определения вероятности наступления случайного события х выглядит следующим образом:
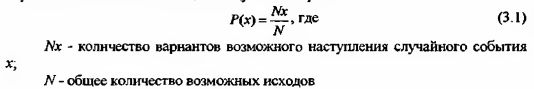
Например. Бросая игральную кость, мы можем получить шесть возможных исходов – выпадение одной из шести граней игральной кости: 1, 2, 3, 4, 5 или 6. Таким образом, можно определить вероятность выпадения одной из гранен, например, 3:
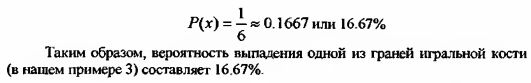
Можно также определить вероятность выпадения одной из двух граней (например, 2 или 3). В этом случае используется правило сложения вероятностей, а вероятность рассчитывается следующим образом:
Р(х или у) = Р(х) + Р(у) = 0.1667 + 0.1667 = 0.3333 или 33.33%,
где Р(х) – вероятность наступления случайного события х (в нашем примере 2);
Р(у) – вероятность наступления случайного события у (3).
Таким образом, вероятность выпадения грани с цифрой 2 или 3 равна 33.33%.
Правило сложения вероятностей используется для зависимых событий, когда одно случайное событие исключает наступление другого случайного события.
Если необходимо найти вероятность одновременного наступления двух и более случайных событий, используется правило умножения вероятностей. При этом все события должны быть независимы друг от друга.
Например. В результате одновременного броска двух игральных костей мы можем получить 36 различных комбинаций: 1-1, 1-2, 1-3, 1-4, 1-5, 1-6, 2-1, 2-2, 2-3 и т.д. Для определения вероятности того, что в результате подбрасывания мы получим на гранях обеих игральных костей по единице, используем правило умножения вероятностей:
Р(х и у) = Р(х) * Р(у) = 0.1667 * 0.1667 = 0.0278 или 2.78%
|



















