|
Предыдущие стратегии и примеры показывают привлекательность попыток торговать волатильностью в отличие от предсказания цен. Однако из-за того, что эти стратегии столь простые, при создании более сложных стратегий вам часто приходится формировать мнение относительно цен. Пришло время обсудить способы, которыми можно наиболее легко изолировать влияние волатильности, и вместе с тем в меньшей степени полагаться на цены в своих стратегиях.


Для этого следует подходить к ситуациям теоретически более подготовленным. Таким образом, этот раздел может показаться сложным. Однако данные понятия не настолько сложны. Я часто говорил, что со статистикой на Уолл-стрите обращаются как с ракетостроением. То есть математика, тривиальным образом понятная студенту колледжа математического профиля, для многих трейдеров кажется насыщенной эйнштейновскими качествами. Более того, многие трейдеры считают: если компьютер что-то сказал, это абсолютная правда. Вы не должны с благоговейным трепетом относиться к тому, что мы сейчас представим.
Это не «скатерть-самобранка» и не абсолютный секрет к успеху. Если бы все было так просто, каждый бы это использовал. Однако рассматриваемое здесь шаг наверх по сравнению с обычным вашим видением опционных стратегий и может привести вас к более основательным и менее рискованным инвестициям.
Чтобы изолировать волатильность, необходимо понять, как изолировать каждую из переменных, влияющих на цену опциона. Ранее в этой главе нами перечислены термины, описывающие меру риска опциона или портфеля для каждой переменной, которая влияет на цену опциона. Поскольку эти показатели риска потенциальных убытков имеют греческие (или звучащие по-гречески) названия, все вместе мы называем их «греки».
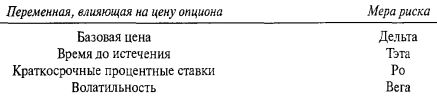
Мы также говорили, что продвинутые трейдеры, применяющие данный подход к нейтральной торговле, ведут наблюдение и за «гаммой» — мерой риска «дельты».
Модель
Основой для вычисления всех указанных показателей и выяснения подразумеваемой волатильности и теоретической стоимости опциона является опционная модель. Существует несколько моделей, доступных для основной публики. То есть их формулы опубликованы в печати и находятся в общественном использовании. Самой ранняя и простейшая из них — модель Блэка-Шоулза — создана в 1973 году этими двумя профессорами. С тех пор многие пытались сделать поправки и улучшения, чтобы дать более точные ответы на вопрос о теоретической стоимости.
Одна из наиболее популярных альтернатив — Биномиальная модель (формула этой модели и несколько примеров даны в Приложении «С»). Она включает намного больше вычислений, чем модель Блэка-Шоулза, но в сегодняшнем мире быстродействующих компьютеров эти вычисления можно выполнить достаточно быстро, хотя далеко не так, как немногие вычисления для модели Блэка-Шоулза. Довольно смешно то, что после всех этих «улучшений» за многие годы более новые модели редко дают «ответы» — то есть стоимости опционов в реальности отличаются от результатов модели Блэка-Шоулза более чем на несколько центов. В сущности, разница между результатами модели Блэка-Шоулза и Биномиальной модели меньше, чем спрэд покупателя-продавца для данного опциона на бирже. Следовательно, нет причин использовать вместо модели Блэка-Шоулза более сложную модель, особенно тем, кто платит комиссионные и не является маркет-мейкером.
Модель иметь необходимо, потому что «греков» нельзя вычислить без нее. Модель — это функция, основанная на пяти переменных, определяющих цену опциона (цена акции, цена исполнения, время до истечения, волатильность и процентные ставки). Из этих пяти лишь цена исполнения всегда неизменна для конкретного опциона. Все другие меняются по мере изменения рыночной ситуации, день за днем. «Греки» измеряют воздействие одной переменной при условии, что все остальные переменные постоянные. Чтобы представить, чем же фактически являются «греки», приведем простой пример.
Предположим, мы пытаемся оценить опцион при следующих исходных данных:
Цена акции: 50
Цена исполнения: 55
Остающееся время: 3 месяца
Волатильность: 25%
Процентная ставка: 6%
При этих допущениях модель Блэка-Шоулза выдаст теоретическую стоимость 1.02. Теперь предположим, что мы оставим все данные теми же самыми, но пересчитаем теоретическую стоимость при цене акции 51. Тогда новые допущения будут следующими:
Цена акции: 51
Цена исполнения: 55
Остающееся время: 3 месяца
Волатильность: 25%
Процентная ставка: 6%
При таком наборе переменных модель Блэка-Шоулза выдаст теоретическую стоимость 1.33.
Сейчас мы вычислили дельту данного опциона. То есть теоретическая стоимость данного опциона выросла на 31 цент при повышении цены акции на один пункт, тогда как все другие переменные остались теми же. Таким образом, дельта равна 0.31.
В действительности для вычисления дельты есть математическое уравнение, устанавливающее, что дельта данного опциона 0.28 при цене акции 50 и равна 0.34 при цене акции 51. Таким образом, первый (менее теоретический) метод дал результат — среднее двух дельт, вычисленных математически. Данный пример указывает, что дельта изменяется всегда, даже если акция движется всего на один пункт. В любом случае можно видеть, что два приведенных метода вычисления дельты принесли очень схожие результаты.
Из предыдущего примера следует, что «греки» вычисляется изменением одной из четырех переменных, подверженных флуктуациям в течение любого торгового дня, пока остальные остаются постоянными. Подобным образом можно измерить изолированный эффект изменения любой одной переменной на цену опциона. Почти все опционные программы проводят вычисления всех «греков» по любому опциону. С математической точки зрения, каждый из «греков» — это частная производная модели по одной из четырех переменных. Не волнуйтесь, если вы не знаете, что такое частная производная — будучи стратегом, вам достаточно знать, как интерпретировать математические результаты, а не как вычислять саму математику. Эта информация важная, поскольку ее можно использовать для создания позиций, нейтральных по отношению к любой одной или нескольким переменным. Однако прежде чем приступить к анализу позиций, рассмотрим сами «греческие» термины.
Дельта
Как вы уже должны знать, дельта опциона — это мера того, как сильно опцион меняется в цене при изменении цены базового инструмента на один пункт. Дельта опциона колл есть положительное число, меняющееся в интервале между 0 и 1, а дельта опциона пут — число отрицательное, меняющееся между -1 и 0.
Дельта опциона уже в некоторой степени обсуждалась и ранее в этой главе, и в Главе 1. В контексте предыдущего примера предположим, что в дополнение к повышению цены акции на один пункт позволим меняться и трем другим переменным: остающемуся времени, волатильности и процентной ставке. Теоретическая стоимость опциона при этом наверняка изменится. Но какая ее часть будет соответствовать данному изменению цены акции? Ответить трудно, но очевидно, что и другие переменные влияют на дельту.
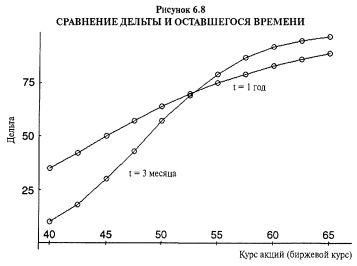
На Рисунке 6.8 показана взаимосвязь дельты и времени. Опцион с большим временем до истечения имеет дельту, меняющуюся достаточно умеренно при движении базового инструмента из далеко "вне денег" (левая сторона графика) в глубоко "в деньгах" (правая сторона графика). Однако для краткосрочного опциона это изменение значительнее, поскольку дельта опциона колл возрастает почти до 1.00 достаточно быстро, когда опцион "в деньгах" (правая сторона; верхняя линия на графике), и дельта падает почти до нуля очень быстро, когда опцион находится "вне денег" (левая сторона; нижняя линия на графике).
В феврале 1995 года, всего за несколько дней до февральского истечения, Motorola объявила о снижении продаж сотовых телефонов, наиболее важного своего продукта. Акция упала более чем на 6 пунктов, с 64 до 58, а внутридневные снижения еще больше. Это случилось за один день до истечения февральских опционов.
Державшие опционы пут "вне денег" имели различные степени успеха, но наиболее драматичной оказалась разница между Февраль-55-пут и Март-55-пут. За один день перед этим объявлением при цене акции 64 (кстати, повысившейся в тот день на 2 пункта) оба этих пута торговались по 1/16 доллара — по минимальной стоимости. Когда на следующий день акция упала (катастрофически), Февраль-55-пут не сдвинулся с места — он по-прежнему торговался по 1/16. Однако Март-55-пут подскочил до доллара, повысившись почти на целый пункт.
Возможно, наиболее сильно сообщение отразилось на Январь(1997)-50-LEAPS-пут, имевший в тот момент почти два года остающейся жизни, но находился на пять пунктов дальше-"вне денег" и превзошел оба указанных пута, повысившись до 1 1/2 пункта. Таким образом, сила временного фактора в качестве воздействия на возможную величину движения опциона ярко продемонстрирована данным реальным примером.
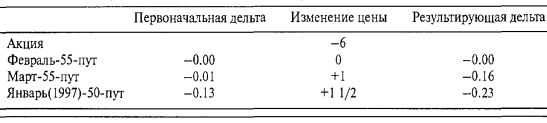
Большое движение акции повлияло и на дельты опционов: Февраль-55-пут перед падением имел дельту 0.00 и после падения по-прежнему показывал дельту 0.00, подтверждая тот факт, что дельта краткосрочного опциона "вне денег" не меняется при движении акции (даже таком большом). Дельта Март-55-пут сдвинулась с -0.01 перед падением акции до -0.16 после падения, увеличившись (в абсолютной величине) на 0.15. Однако более долгосрочный опцион, несмотря на его более сильное изменение в цене, имел меньшую флуктуацию дельты, поскольку его дельта сдвинулась с -0.13 до -0.23, изменившись всего на 0.10. Эти факты подытожены в следующей таблице:
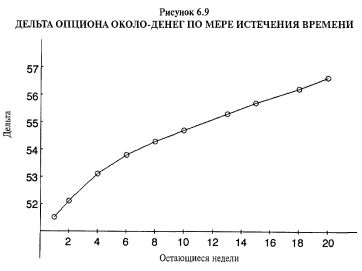
Ранее мы упоминали, что дельта опциона "около денег" не является в точности равной одной второй (0.50). Скорее, она несколько больше. Еще более интересен тот факт, что дельта этого опциона колл "около денег" изменяется с течением времени. Рисунок 6.9 представляет график дельты данного колла, показывая это достаточно ясно. Пут должен демонстрировать схожее изменение, но дельта опциона пут с течением времени двинется в противоположном направлении, изменяясь, например, с -0.43 почти до -0.50 (дельта опциона пут равна дельте опциона колл минус 1). Следовательно, данный пут "около денег" становится чувствительнее к изменениям цены базовой ценной бумаги по мере приближения даты истечения, тогда как колл приобретает меньшую чувствительность. Однако в обоих случаях величина этого различия мала.
Нами уже показано, что движение цены базового инструмента заставляет дельту меняться и течение времени также изменяет дельту. Третий основной фактор влияния на дельту опциона колл — волатильность. Существует два типа волатильности: подразумеваемая и историческая. Историческая волатильность — это мера того, как быстро менялась цена базового инструмента. Подразумеваемая волатильность — это волатильность, которую в текущий момент демонстрируют опционы — своего рода проекция будущей волатильности. Любая из них может влиять на дельту опциона, но именно подразумеваемая волатильность обычно оказывает более впечатляющий, но краткосрочный эффект.
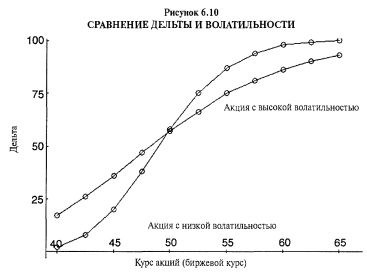
Опционы на низковолатильную акцию имеют лишь небольшую величину временной премии. Таким образом, опционы "вне денег" не столь чувствительны к краткосрочным движениям акции, а опционы "в деньгах" — очень чувствительны. Это означает, что дельта опциона "вне денег" на низковолатильную акцию невелика, возможно, близка к нулю, а дельта соответствующего опциона "в деньгах" велика. График на Рисунке 6.10 демонстрирует данный факт. Это в некоторой степени напоминает поведение опционов с небольшим сроком остающейся жизни, что уже обсуждалось ранее. С другой стороны, если базовый инструмент очень волатильный, его опционы "вне денег" окажутся более чувствительными к изменениям цены базовой ценной бумаги, а опционы "в деньгах" не смогут измениться на целый пункт при изменении базы на один пункт, потому что они обладают премией временной стоимости. Это также показано на Рисунке 6.10 и напоминает по своему характеру поведение долгосрочного опциона.
С другой стороны, подразумеваемая волатильность может меняться очень быстро. То есть восприятие рынком будущей волатильности может измениться за ночь. Следующий пример показывает, как это происходит.
В 1994 году Gensia Pharmaceuticals, начинающая компания по производству лекарств, была типичной акцией с высокой волатильностью. Ее нормальная волатильность составляла примерно 70% в год, что достаточно высокий уровень (рынок в целом обычно имеет волатильность между 10 и 15%). В июле 1994 года Администрация продовольствия и лекарств (FDA) объявила, что собирается провести слушание по основному лекарству Gensia. Цена ее акций соскользнула со значений около 10 до 8, а затем быстро вскарабкалась обратно к 10 в течение следующего месяца. Фактически ценная бумага была неволатильной, а опционы — волатильными. Подразумеваемая волатильность опционов немедленно и впечатляюще подскочила, поднявшись в область 130— 140%. Это произошло потому, что трейдеры знали: решение FDA «либо создаст, либо развалит» («make or brake») данную компанию. В конечном счете, в октябре FDA приняла решение против Gensia и акция за ночь упала в цене на 50%. Однако как только все это (ожидание) закончилось, подразумеваемая волатильность изменилась за ночь со 130 до 70%, поскольку у трейдеров больше не было необходимости дисконтировать такое волатильное событие, как принятие FDA решения относительно будущего компании.
Подразумеваемая волатильность может по многим причинам испытывать подобные внезапные скачки. Одна из них — важное корпоративное объявление. Например, решение FDA или судебное решение. Другая причина впечатляющего повышения подразумеваемой волатильности — восприятие изменения будущей цены базового инструмента. Для акций это обычно связано со слухами о поглощении; для зерновых фьючерсов — обусловлено ожиданиями плохой погоды. Когда возникают подобные ситуации, для изменения волатильности какой-то определенной причины нет (как, например, решение FDA). Опционные трейдеры могут вдруг просто обнаружить впечатляющее изменение цен опционов даже при отсутствии новостей, способных быть причиной этого, и когда явного движения цены базовой ценной бумаги тоже нет. В сущности, дельта такого опциона меняется очень сильно. Можно представить себе этот сценарий, рассмотрев предыдущий график и предположив, что дельта опциона находилась на одной линии на графике, а потом внезапно переместилась на другую, притом, что цена акции не изменилась вообще.
Стратегу важно понимать эти концепции, поэтому ему надо знать, что любая «нейтральная» позиция не безрисковая — она нейтральна лишь по отношению к одной или нескольким переменным, которые изначально были нейтрализованы. Последующие изменения значений других переменных отрицательно повлияют на эту нейтральность. Ранее в этой главе мы видели это в примерах, касающихся дельты, когда изначально дельта-нейтральная позиция становилась существенно ненейтральной при изменении цены базовой акции.
Вега
Это обозначение присвоено «греческому» термину, описывающего, как изменение волатильности влияет на цену опциона (снова при условии, что все остальные переменные постоянные). Поскольку сейчас обсуждаемая нами «волатильность» просто значение, вводимое в модель оценивания, мы на самом деле говорим о подразумеваемой волатильности. Вероятно, большинство опционных трейдеров не знакомы с термином «вега», а следовало бы, поскольку ничто не оказывает на цену опциона такого впечатляющего воздействия, как волатильность. В самом деле, как было неоднократно показано в данной книге, изменение подразумеваемой волатильности может краткосрочно сильно влиять на цену опциона.
Тема данной главы — торговля волатильностью, поэтому в последующих разделах о веге говорится достаточно много. Если измерить эффект, который оказывает на позицию изменение волатильности, нам станет известно, насколько большой риск мы принимаем на себя при торговле волатильностью.
Предположим, как нами уже делалось ранее в этой главе, что мы наблюдаем нахождение волатильности определенной ценной бумаги в интервале между 20 и 34%. Далее, скажем, в текущий момент волатильность составляет 32%, и мы рассматриваем возможность продажи волатильности.
Допустим, нами создается позиция, имеющая (позиционную) вегу -5.00. То есть при каждом повышении волатильности на один пункт (например, с 32 до 33%) мы будем терять $500. Это предполагает, что вега -5.00 стоит $500, как было бы в случае любого опциона, размер контракта которого составлял $100 за пункт. Однако, если это опцион на фьючерс с более крупным размером контракта, риск, связанный с волатильностью, был бы равен размеру контракта, помноженному на -5.00.
Здесь вега отрицательная, отражая тот факт, что падение волатильности являлось для позиции прибыльным, в то время как рост волатильности наносил ущерб. Если мы на самом деле уверены в сохранении имеющегося торгового интервата волатильности с вершиной в 34%, то наш риск, связанный с волатильностью, составляет два пункта (с 32 до 34%), или $1000.
Если мы ждем снижения волатильности, например, до 27%, что является центром прошлого торгового интервала волатильности, в этом случае можно получить прибыль $2500 ($500 умножить на 5 пунктов снижения волатильности: с 32 до 27%).
Тогда в целом эта позиция имеет риск $1000 и потенциал прибыли $2500, что измерено с помощью веги. Конечно, как мы знаем, на позицию могут влиять и другие факторы, включая способность подразумеваемой волатильности двигаться до более высоких уровней, чем достигнутые ранее. Тем не менее этот пример показывает: используя вегу, можно оценить риск позиции, связанный с волатильностью.
Далее в этой главе исследованы способы изоляции волатильности от других переменных для создания позиции, нейтральной к рынку в отношении всех переменных, за исключением волатильности.
Тэта
Тэта — мера временного «упадка» опциона, то есть снижения стоимости ценных бумаг в портфеле инвестора — вводится отрицательным числом, отражая тем самым, что при прохождении одного дня стоимость опциона будет снижаться. Тэта полезна для описания, как именно течение времени влияет на портфель опционов. Если в вашем портфеле много коротких (непокрытых) опционов, у вас будет очень большая положительная тэта, потому что время ваш союзник. С другой стороны, если вы владеете большим количеством опционов, тэта вашего портфеля будет отрицательной, в точности описывая убыток, который можно ожидать ежедневно в связи с временным распадом.
Ро
Ро измеряет эффект, который оказывает на цену опциона изменение процентных ставок. Процентной ставкой, используемой для оценивания опционов, является краткосрочная безрисковая процентная ставка, которой обычно считается ставка по 90-дневным казначейским векселям. Для краткосрочных опционов в позициях большинства трейдеров «ро» очень небольшое число и поэтому справедливо игнорируется большинством трейдеров. Для более долгосрочных опционов, таких как LEAPS, «ро» имеет большее значение. В самом деле, чем дольше жизнь опциона, тем важнее процентные ставки. На Рисунке 6.11 показаны три кривые теоретической стоимости двухлетнего LEAPS-опциона. Верхняя кривая изображает цены при процентной ставке 9%, средняя кривая — при процентной ставке 6%, а нижняя кривая — при ставке 3%. По расстоянию между этими кривыми можно видеть, что эффект от процентных ставок в данном случае значителен.
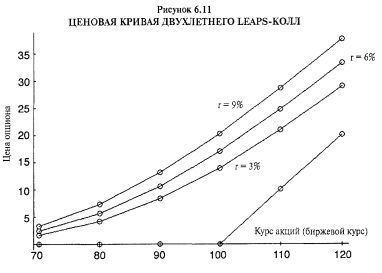
Конечно, вы не увидите мгновенного изменения краткосрочных процентных ставок на 3%, но можете увидеть результат такого изменения за достаточно короткий период времени, если ФРС агрессивно пытается повысить или снизить ставки.
В течение 1994 года ФРС повышала учетную ставку несколько раз, пытаясь охладить экономику, считавшуюся перегретой. Во время этого повышения безрисковая ставка выросла с 3 до 5.5% примерно за 10 месяцев. Обычно при росте ставок цены акций спотыкаются. Девяносто четвертый год не был исключением. В тот год имели место три или четыре достаточно крутых снижения рынка в целом, и за год основные индексы немного ушли вниз.
По-настоящему выиграли от этого роста ставок LEAPS-опционы. В самом деле, рост ставок за восемь месяцев фактически нивелировал большую часть временного «упадка» долгосрочных опционов. По существу, цены передвинулись с нижней линии на графике (Рисунок 6.11) на среднюю линию, хотя прошло всего восемь месяцев.
Возвращение к гамме
С помощью четырех предыдущих показателей можно определить, как ваши опционные позиции или ваш опционный портфель в целом будут реагировать на рыночные изменения. Однако некоторые теоретики считали, что этого недостаточно, потому что два из них — дельта и вега — могут изменяться настолько быстро, что их трудно нейтрализовать. Итак, они полагали: если бы можно было измерить, например, изменение дельты, это было бы полезным. Это и есть гамма, ранее описанная в этой главе. Гамма показывает, насколько сильно меняется дельта опциона, когда базовая ценная бумага отклоняется в цене на один пункт. По существу, это мера того, насколько быстро меняется дельта. Таким образом, если бы гамму и дельту можно было нейтрализовать, то даже при изменении базовой цены опционная позиция, о которой идет речь, продолжала бы оставаться дельта-нейтральной. В конечном счете, если цена базовой ценной бумаги сдвинется достаточно далеко, то и гамма, и дельта должны будут стать какими-то ненулевыми значениями, и позиция обязательно потеряет свою нейтральность. Тем не менее дельта- и гамма-нейтральная позиции имеют гораздо больший шанс остаться дельта-нейтральными, чем позиция, изначально только дельта-нейтральная.
Гамма связана и с другими показателями риска (фактически все факторы, определяющие цену опциона, взаимосвязанные). Рисунок 6.12 показывает, как связана гамма с величиной времени, остающегося до истечения обсуждаемого опциона. Если до истечения остается много времени, гамма относительно стабильное число и для опциона "в деньгах", и для опциона "вне денег". Это показывает нижняя кривая на графике.
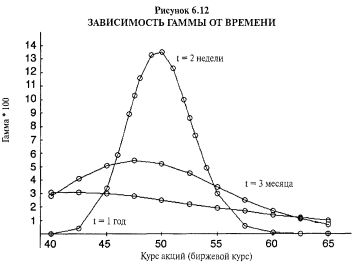
Этот факт можно представить и в табличной форме. Таблица 6.1 содержит данные об опционе (имеет один год до истечения и цену исполнения 50) — его теоретическую стоимость и дельту. Гамма просто равна разнице дельт при движении базовой акции на один пункт. Таким образом, в данной таблице показана наблюдаемая гамма (фактическая разница дельт), а не математически вычисляемая гамма. По существу, обе они одинаковые.
Вы можете наблюдать, что для этого долгосрочного опциона гамма остается достаточно стабильной. По мере роста акции дельта возрастает достаточно единообразно (или снижается единообразно при падении акции). Однако если рассматривать краткосрочный опцион, ситуация существенно меняется. На Рисунке 6.12 показано, что гамма одномесячного опциона ведет себя довольно стремительно, когда цена акции близка к цене исполнения. Таблица 6.2, похожая на предыдущую, показывает ситуацию для одномесячного опциона.
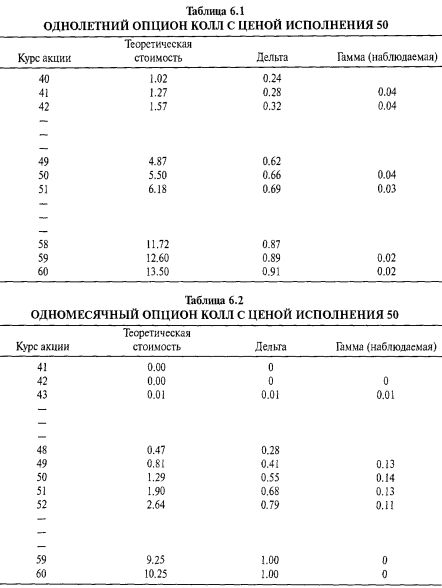
В случае этого краткосрочного опциона гамма стабильна и почти равна нулю для опционов лишь немного "в деньгах" или "вне денег". Это логично. Например, опцион немного "вне денег", имеющий очень мало времени до истечения, обладает дельтой, близкой к нулю. Даже если базовый инструмент вырастет на один пункт, его дельта по-прежнему будет очень близка к нулю. Таким образом, рост базовой цены на один пункт почти не повышает дельту — это всего лишь другой способ сказать, что его гамма тоже почти равна нулю. То же самое справедливо для опциона "в деньгах". В этом случае дельта очень близка к 1.00, и движение базовой цены на один пункт не сильно изменит дельту. Следовательно, опять же гамма почти равна нулю, поскольку дельта не меняется при движении базовой цены на один пункт.
Однако рядом с ценой исполнения ситуация намного интереснее. Дельта меняется достаточно быстро, особенно для краткосрочного опциона на акцию с низкой волатильностью. Это тоже логично, поскольку рядом с датой истечения временная стоимость опциона исчезает быстро. Таким образом, небольшое повышение цены акции при ее движении выше цены исполнения очень быстро приведет к повышению дельты от значения чуть выше 0.50 до очень высокого уровня. Итак, гамма связана со временем и волатильностью.
Гамма- и дельта-нейтральность
Следующий логичный шаг в построении позиции, остающейся нейтральной по отношению к цене, это создание позиции, нейтральной и относительно дельты, и относительно гаммы. В этом случае позиция не будет обладать большим риском в отношении ценовых изменений базового инструмента. Построить такую позицию довольно просто, хотя для многих трейдеров это кажется пугающим. На самом деле необходимо сделать всего два шага: (1) создать гамма-нейтральную позицию; (2) нейтрализовать дельту. Второй шаг всегда можно выполнить с помощью (эквивалентных) единиц контрактов на базовую ценную бумагу.
Предположим, в начале года акция торгуется по 98 и трейдер заинтересован в создании гамма- и дельта-нейтральной позиции с помощью следующих трехмесячных опционов:

Гамма небольшое число, поэтому для нее необходимо использовать формат как минимум с тремя знаками после запятой, особенно если вы торгуете в больших объемах.
Теперь для создания гамма-нейтральной позиции необходимо просто вычислить отношение двух гамм, о которых идет речь, для определения нейтральной пропорции. В этом случае нейтральной позицией будет покупка двух Март-100-колл на каждые три продаваемые нами Март-110-колл, поскольку пропорция их гамм именно такая: 2 к 3 (0.020 к 0.030). Эта позиция будет иметь ненулевую дельту, и в этом примере мы разберемся с нейтрализацией этой дельты.
Допустим, наша реальная сделка охватывает покупку 200 Март-100-колл и продажу 300 Март-110-колл. Эта позиция имеет следующую ESP, или дельту позиции:

Чтобы нейтрализовать эту позицию, мы могли бы продать (шорт) 2500 обыкновенных акций против данного опционного спрэда либо использовать наше знание эквивалентных позиций и вместо этого продать 25 Март-100-колл и купить 25 Март-100-пут. Если бы мы использовали опционы, наша результирующая позиция оказалась бы следующей:
Лонг 175 Март-100-колл
Шорт 300 Март-110-колл
Лонг 25 Март- 100-пут
Использование эквивалентной опционной позиции не меняет гамму вообще. Ни акция, ни эквивалентная позиция совсем не имеют гамму (то есть гаммы Март-100-колл и март-100-пут равны и компенсируют друг друга, когда мы покупаем и продаем одинаковое количество этих опционов).
В предыдущем примере принято допущение: мы используем гаммы для создания нейтральной позиции, в основе которой пропорциональное надписание опционов колл. В самом деле, мы могли бы сделать и наоборот. Любая из этих позиций являлась бы гамма-нейтральной.
Купить 2 Март-100-колл
Продать 3 Март-110-колл
или
Продать 2 Март-100-колл
Купить 3 Март-110-колл
Мы выбираем позицию в зависимости от наших целей. Если наши намерения в продаже волатильности, мы будем использовать первую позицию — пропорциональное надписание из опционов колл. Однако если мы пытаемся купить волатильность, то будем использовать вторую позицию — обратный спрэд. В этом примере не виден риск потенциальных убытков данной позиции по отношению к волатильности. Но из того, что уже показано в этой главе, нам известно: пропорциональное надписание опционов колл — одна из стратегий, используемых при продаже волатильности, тогда как обратный спрэд — это стратегия, используемая для покупки волатильности. Вскоре мы обратимся к вопросу риска потенциальных убытков гамма- и дельта-нейтральной позиции по отношению к риску потенциальных убытков.
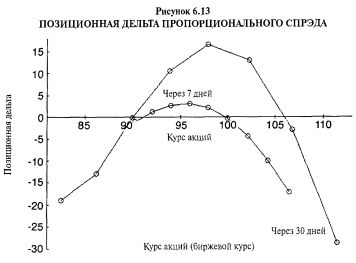
Тем не менее исследуем сначала данную позицию пристальнее, чтобы увидеть, какими именно характеристиками обладает гамма- и дельта-нейтральной позиция. На Рисунке 6.13 показана дельта этой позиции при различных ценах акции. Более горизонтально выглядящая линия демонстрирует, какой была бы дельта по прошествии семи дней. Другая линия с более размашистыми колебаниями показывает, какой оказалась бы дельта через 30 дней. Даже несмотря на то, что изначально позиция являлась дельта- и гамма-нейтральной, она на самом деле с течением времени приобретает дельту, особенно когда базовая акция впечатляюще меняется в цене. Однако следует помнить: позиция в данном примере достаточно крупная, поэтому приобретенные дельты не являются такими уж большими. В самом деле, по прошествии семи дней дельты оставались довольно незначительными — в этом преимущество гамма- и дельта-нейтральной позиции.
Дельты остаются относительно «без движения» в некотором интервале — примерно до уровня цены 100 в течение семи дней и примерно до уровня цены 107 за 30 дней. Это означает, что вам, вероятно, не пришлось бы корректировать позицию, если бы акция не выросла выше этих цен. Свыше этих уровней позиция становится достаточно дельта-короткой. После 30 дней крупное движение в нижнюю сторону вызывает приобретение позицией короткой дельты (из-за наличия длинной позиции по 25 Март-100-пут). В этом случае нейтральный трейдер тоже мог бы захотеть скорректировать позицию.
Достаточно сказать, что дельта позиции в данном примере гораздо стабильнее, чем у типичного пропорционального надписания опционов ком в отношении 1-к-2 (например, с покупкой 100 Март-100-колл и продажей 200 Март-110-колл, что лишь дельта-нейтральная позиция).
Фактическая позиция, построенная нами с помощью этой гамма- и дельта-нейтральной позиции, по большому счету является пропорциональным надписанием опционов колл, но она имеет несколько дополнительных путов, добавленных для увеличения потенциала прибыли в нижней стороне. Кроме того, отношение длинных к коротким опционам колл меньше, чем вы бы имели просто в дельта-нейтральной позиции (1.75-к-3 вместо 1-к-2). Поэтому данная позиция не имеет большого риска потенциальных убытков в отношении непокрытых опционов.
Если вас интересует, как выглядит эта гамма- и дельта-нейтральная позиция с точки зрения прибылей и убытков, на Рисунке 6.14 показана ее прибыльность на момент истечения (прямые линии) и через 30 дней (кривая линия). Этот график построен при допущении, что волатильность не изменяется, поэтому прибыли и убытки накапливаются за счет движения цены акции и времени. В действительности мы бы занимали такую позицию лишь в том случае, если бы ожидали снижение волатильности. Сейчас мы увидим, как это событие влияет на прибыльность.
Позиция в нашем примере изначально имела риск потенциальных убытков по отношению к растущей волатильности, то есть данная позиция короткая по волатильности, или, выражаясь в греческих терминах, имеет отрицательную вегу. Это именно то, чего бы мы хотели в случае продажи волатильности. Чтобы увидеть количественную сторону этих утверждений, продолжим предыдущий пример, включив теперь в наши вычисления волатильность.
Сделаем еще одно допущение относительно этой позиции. Предположим, трейдер сделал наблюдение: волатильность данной акции обычно торгуется в интервале между 20 и 30%. Сейчас, при волатильности 30%, он хочет создать гамма- и дельта-нейтральную позицию с целью продажи волатильности. Позиция в нашем примере как раз то, что нам нужно.
Приведенные ниже данные в точности соответствуют предыдущему примеру, за исключением того, что теперь можно также видеть вегу каждого опциона. Вега — это величина, на которую будет возрастать цена опциона при (мгновенном) повышении подразумеваемой волатильности на один процент. В эту таблицу также внесены данные по опциону пут.

Наша изначальная позиция: 175 длинных Март-100-колл, 300 коротких Март-110-колл и 25 длинных Март- 100-пут — была дельта- и гамма-нейтральной, но имела риск потенциальных убытков по отношению к волатильности. Можно легко вычислить эту экспозицию, используя вегу опционов.

Вега всегда положительное число. Таким образом, длинные опционные позиции (Март-100-колл и Март-100-пут в данном примере) имеют положительную вегу, в то время как короткие опционные позиции обладают отрицательной позиционной вегой.
Вега предыдущей позиции показывает, что если подразумеваемая волатильность падает на 1%, например, с 30 до 29%, то позиция будет иметь прибыль $900. Конечно, это моментальное измерение, и на него влияют изменения цены акции и истечение времени. На Рисунке 6.15 показана прибыль через 30 дней — пока нижняя кривая осталась такой же, как мы видели на предыдущем графике прибылей. Это и есть прибыль, если волатильность не изменяется. Верхняя кривая показывает, что произойдет, если волатильность снизится до 25%, примерно к середине 20—30-процентного интервала, который мы допустили в данном примере.
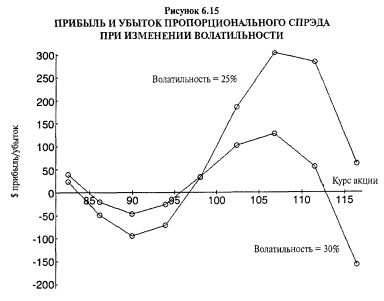
Вы можете видеть, какую большую дополнительную прибыль принесло бы данной позиции снижение волатильности, когда акция выше 98.
Этот достаточно подробный пример показывает, насколько прибыльной может быть гамма- и дельта-нейтральная позиция при снижении подразумеваемой волатильности. Но при этом, как правило, следует придерживаться более нейтрального взгляда в отношении базовой цены, чем при простом пропорциональном спрэде из опционов колл. Посмотрев на каждую из наших пяти предпочтительных дельта-нейтральных стратегий для торговли волатильностью, можно увидеть, как они будут выглядеть в качестве гамма- и дельта-нейтральных позиций. Эта трансформация достаточно интересна. Однако прежде чем сделать это, предлагаем вам еще один кусочек общей мозаики, а именно: как построить гамма- и дельта-нейтральную позицию с риском потенциальных убытков по отношению к волатильности.
Это легко достигается решением двух уравнений с двумя неизвестными и последующей корректировкой любой остаточной дельты. Как только вы говорите «два уравнения с двумя неизвестными», многие начинают паниковать. Расслабьтесь. Есть простые способы их решения. Прежде всего, это всего лишь алгебра общеобразовательной школы. Если в вашей семье есть учащийся школы или института, по всей вероятности, он сумеет решить эту проблему. Если быть реалистичнее, есть простые программы, решающие два уравнения с двумя неизвестными. Они доступны в форме пробного использования с последующей оплатой, или, возможно, распространяются бесплатно. Если вы все-таки не найдете ни одной такой программы, позвоните нам. Мы вышлем вам одну из них при условии оплаты вами почтовых расходов.
Продолжим тот же самый пример для иллюстрации данного вопроса. Мы собираемся прийти, по сути, к той же позиции, как и раньше. Но в данном случае подойдем к ситуации в целом с конкретной идеей, связанной с приемлемой нами величиной риска. В более раннем примере нами просто создавалась гамма- и дельта-нейтральная позиция, а затем рассматривалось, насколько большой являлась вега.
Предположим, вы хотите создать пропорциональный спрэд из опционов колл с помощью мартовских опционов — как мы делали раньше — и допускаете риск $1000 на каждый пункт роста волатильности. Конечно, это значит, что у вас будет прибыль $1000 от каждого снижения волатильности на один пункт и именно отсюда возникнут ваши прибыли. Выражаясь в «греческих» терминах, риск в $1000 на каждый пункт роста волатильности означает, что данная позиция имеет вегу, равную -10.00.

Выразим через «х» число покупаемых опционов Март-100-колл, а через «у» — число продаваемых Март-110-колл. Помните, что мы хотим оставаться гамма-нейтральными и иметь вегу -10. Тогда уравнения будут выглядеть следующим образом.
Гамма-нейтральность: 0.030х + 0.020у = 0
Вега-риск: 0.180х + 0.150у = -10
Решая систему этих уравнений, получим: х = 222 и у = -333. Это означает: нам надо купить 222 Март-100-колл и продать 333 Март-110-колл. При этом позиция будет иметь некоторую дельту. Поскольку мы хотим быть дельта-нейтральными, необходимо избавиться от этой дельты.

Можно либо продать коротко 2800 акций, либо использовать эквивалентную опционную позицию — продать 28 Март-100-колл и купить 28 Март-100-пут. В результате получим следующую позицию:
Лонг 194 Март-100-колл
Шорт 333 Март-110-колл
Лонг 28 Март-100-пут
Полученная позиция имеет большое сходство с позицией из предыдущих примеров. Она немного больше, потому что мы допустили вега-риск в $1000 на пункт, в то время как в других примерах он $900 на пункт.
Теперь, когда мы определились с теорией создания соответствующей позиции, рассмотрим стратегии торговли волатильностью. Предыдущий пример был несколько упрощенным — в нем ограничен выбор используемых в спрэде опционов колл всего двумя из них: — Март-100 и Март-110. В реальности, когда мы ищем возможности продажи волатильности, то стоим перед выбором из большего числа опционов. Разумно предположить, что для нас имелась возможность использовать в качестве длинной стороны нашего спрэда колл "около денег", но все равно остается несколько вариантов выбора подлежащего продаже опциона колл "вне денег". Обычно стратег может сузить процесс отбора до очень небольшого числа альтернатив, но, как мы увидим в следующем примере, бывают случаи, когда отсев «неправильных» опционов меняет позицию настолько, что она уже не устраивать стратега.
Одна из стратегий продажи волатильности, интересующая многих людей, — короткая непокрытая комбинация. Что происходит с этой позицией, когда вы нейтрализуете гамму? Следующий пример иллюстрирует данную ситуацию. Мы начнем с показа гамма- и дельта-нейтральной позиции с определенным вега-риском, основанной на продаже комбинации.
Допустим, как и в предыдущих примерах, трейдер хочет продать волатильность, в текущий момент находящуюся на уровне 30%, но которая обычно торгуется в интервате между 20 и 30%. Он допускает связанный с волатильностью $ 1000 риск на каждый пункт ее роста. Однако в этом примере трейдер хочет использовать для решения своей задачи продажу комбинации. В таких случаях мы предпочитаем использовать в качестве короткой стороны позиции комбинации (двух цен исполнения) вместо стрэддла.
При цене акции 98 трейдер рассматривает в качестве продажи комбинации продажу Март-95-пут и Март-105-колл, а затем ищет возможность хеджировать эту продажу покупкой опционов "вне денег". В этом примере он собирается использовать в качестве хеджа покупку комбинации "вне денег": опционные контракты Февраль-90-пут и Февраль-110-колл. Когда трейдер для защиты короткой комбинации покупает комбинацию "вне денег", подобную указанной, говорят, что он покупает «крылья» («wings»).
На 2 января цена акции «XYZ» составляет 98 и имеются следующие данные:

Все значения положительны, за исключением дельт опционов пут. Как и раньше, у трейлера будет два уравнения — одно для гаммы и одно для веги. Но похоже, что у него четыре неизвестных, поскольку опционов четыре. На самом деле он может рассматривать ситуацию как имеющую два неизвестных: одному из них соответствует продажа мартовской комбинации, а другому — покупаемая в качестве хеджа февральская комбинация. С помощью такого упрощения он замещает сумму компонентов в каждом уравнении.
Итак, пусть «х» = число продаваемых мартовских комбинаций, а «у» = число покупаемых февральских комбинаций. Тогда наши два уравнения принимают вид:
Гамма-нейтральность: (0.027 + 0.028)х + (0.025 + 0.024)у = 0
Вега-риск: (0.167 + 0.170)х + (0.096 + 0.095)у = -10
Решая систему этих уравнений, получим х = -81 и у = 91. То есть если трейдер продает 81 мартовскую комбинацию, ему следует купить в качестве хеджа 91 февральскую комбинацию. При желании он может вычислить гамму и вегу позиции, чтобы убедиться, что они удовлетворяют его критериям — гамма-нейтральности и вега-риску -10.
Дельту этой позиции можно вычислить следующим образом:
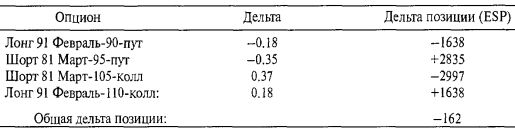
Таким образом, позиция по существу дельта-нейтральная. Если трейдер хотел быть по-настоящему точным, он мог бы купить 100 или 200 единиц базового инструмента, чтобы нейтрализовать эту дельту, но с практической точки зрения это необязательно.
Позиция, к которой мы пришли в данном примере, немного отличается от той, что вы могли ожидать получить. «Нормальная» ее часть состоит в хеджировании продажи комбинации через покупку комбинации из опционов, находящихся дальше "вне денег". Однако необычно в этой позиции то, что длинные опционы истекают прежде, чем короткие. При такой конфигурации соображения, связанные с маржой, могут существенно отличаться. В случае опционов на фьючерсы длинные опционы считаются «покрывающими» короткие опционы до тех пор, пока длинные не истекут, так что маржа равна просто разнице (спрэду) маржевых требований (the spread requirements). Однако в случае с опционами на акции или индексы, по которым до сих пор действуют тяжелые и нелогичные маржевые требования, короткие опционы считаются непокрытыми (за исключением случая, когда трейдер получает маржевые требования, действующие для маркет-мейкеров, то есть когда трейдер торгует в интересах участника биржи).
Необходимость обеспечивать короткие опционы маржой в качестве коротких опционов делает маржевое требование очень большим — гораздо больше соответствующего риска. Очевидно, что независимо от того, насколько сильно изменится базовая цена до истечения длинных опционов — в данном примере февральских, — эти длинные опционы обеспечат защиту против крупных убытков. То есть убытки ограниченные. Абсурдно, что это не учитывается в требованиях к обеспечению.
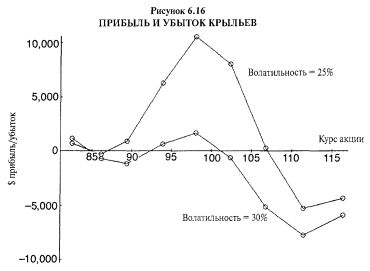
Маржевые требования не уменьшают потенциал прибыли самой позиции, хотя, конечно же, снижают ставку доходности. На Рисунке 6.16 показано, как бы выглядела позиция из предыдущего примера на момент февральского истечения, то есть при завершении жизни длинных опционов. Нижняя кривая показывает прибыли в случае, если волатильность останется неизменной на уровне 30%, в то время как верхняя кривая показывает более высокие прибыли, доступные в случае снижения волатильности до 25% — к середине предполагаемого интервала подразумеваемой волатильности. Снова очевидно, что, даже несмотря на изначальную гамма- и дельта-нейтральность данной позиции, она приобретает риск в связи с прохождением достаточного времени и движением базовой акции. Тем не менее эта позиция обладает значительно меньшим риском, чем просто продажа непокрытой комбинации, имеющая неограниченный риск в случае слишком большого движения базовой ценной бумаги в любом направлении.
Вы можете поинтересоваться, почему в качестве хеджа для данной короткой комбинации мы используем февральские опционы вместо более долгосрочных. Причина в следующем: чтобы начать с продажи непокрытой комбинации и превратить ее в дельта- и гамма-нейтральную позицию покупкой «крыльев», необходимо, чтобы крылья истекали прежде истечения короткой комбинации. Следующий пример показывает, как бы выглядела гамма- и дельта-нейтральная позиция, если бы вы использовали на стороне покупки более долгосрочную комбинацию.
Используя те же самые допущения, что и в предыдущем примере, касающиеся волатильности и желания создать гамма-нейтральную позицию с вега-риском $1000 на пункт на 2 января, при цене XYZ равной 98, существовала следующая статистика:

Мы снова составляем два уравнения с двумя неизвестными, складывая значения соответствующих показателей для каждой комбинации. Пусть «х» = число продаваемых мартовских комбинаций, а «у» = число покупаемых апрельских комбинаций. Тогда два уравнения принимают следующий вид:
Гамма-нейтральность: (0.027 + 0.028)х + (0.019 + 0.022)у = 0
Вега-риск: (0.167 + 0.170)х+ (0.170 + 0.192)у = -10
Решая систему этих уравнений, получаем х = 61 и у = -90. С помощью этих данных, когда мы составляем и решаем простую систему двух уравнений с двумя неизвестными, мы имеем решение, дающее нам абсолютно другую позицию. Теперь «х» положительное число, что означает наше намерение покупать мартовскую комбинацию и продавать апрельскую комбинацию. В сущности, мы создаем два пропорциональных надписания: одно из опционов колл, второе — из путов.
Лонг 67 Март-95-пут
Шорт 90 Апрель-90-пут
и
Лонг 67 Март-105-колл
Шорт 90 Апрель-110-колл
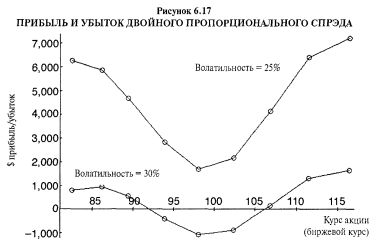
Эта позиция полностью отличается от изначально планированной нами, но это единственный способ создания гамма-нейтральной позиции с требуемой вегой из четырех выбранных нами опционов. На Рисунке 6.17 показано, как она выглядит через 30 дней. Снова нижняя кривая — это прибыли и убытки в случае неизменности подразумеваемой волатильности, в то время как верхняя кривая показывает результаты в случае снижения подразумеваемой волатильности до 25%.
Мы пока никак не решили вопрос с маржой. Как и в предыдущем примере, у нас по-прежнему короткая позиция по более долгосрочным опционам (в данном случае — по апрельским опционам), поэтому данная позиция потребует достаточно большой величины обеспечения.
Причина, по которой эта позиция принимает несколько неожиданную форму, крупная вега апрельских опционов. Для создания позиции с отрицательной вегой — нашим изначальным намерением — практически невозможно купить эти апрельские опционы, поскольку их вега настолько велика. Объединенная вега мартовских опционов равна 0.337, а объединенная вега апрельских опционов выше, составляя 0.362. Это означает, что при каждом снижении волатильности на один пункт мартовская комбинация потеряет примерно 34 цента, но апрельская комбинация потеряет еще больше — 36 центов. Таким образом, продавать мартовскую комбинацию и покупать апрельскую комбинацию не имеет смысла, если мы хотим сделать деньги на снижении волатильности.
Данный пример показывает нечто очень интересное: часто очень трудно «угадать» гамма-нейтральную позицию с риском волатильности, который вы хотите. Но с помощью «греков» можно увидеть в точности структуру, необходимую для достижения ваших целей.
В этой главе мы затратили значительное время на подведение фундамента под нашу стратегию: наша цель торговля волатильностью и по возможности с максимально уменьшенном риском при ценовых изменениях базового инструмента. С помощью «греков» мы гарантированно занимаем позицию, соответствующую нашим целям.
Я часто видел трейдеров, желавших добиться того же самого, что мы описали в этой главе, и которые занимали позицию, выглядевшей работающей, а на самом деле она не работала. Обычно, если мы решаем продать комбинацию для получения прибыли за счет нашего ожидания снижения волатильности, то возможный вариант создания защиты в будущем — это покупка крыльев, истекающих в то же самое время или в более позднем месяце. Предыдущий пример показывает ошибочность такого рассуждения. В действительности покупкой таких крыльев мы по существу сводим на нет наш прибыльный потенциал от снижения волатильности.
Итак, мы увидели, как выглядят две наиболее распространенные стратегии продажи волатильности — пропорциональный спрэд и непокрытая короткая комбинация, преобразованные в гамма- и дельта-нейтральные позиции. Теперь рассмотрим, как можно оперировать основными стратегиями покупки волатильности — длинным стрэддлом, обратным спрэдом и календарным спрэдом, когда речь идет о создании гамма- и дельта-нейтральных позиций.
Календарный спрэд. Не вдаваясь в такие детали, как в предыдущих примерах, покажем лишь, каким образом выглядела бы позиция календарного спрэда, гамма- и дельта-нейтральная при соответствующей экспозиции по отношению к волатильности (вега равна +10 — то есть теперь вега положительная) на 2 января при цене XYZ, равной 100, и волатильности 20%:
Лонг 52 Июнь-100-колл
Шорт 44 Март-100-колл
Лонг 15 Июнь-100-пут
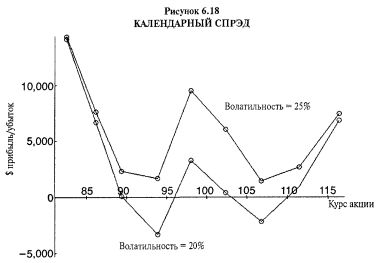
Итак, данная позиция похожа на обычный календарный спрэд, за исключением того, что на длинной стороне спрэда небольшое число дополнительных длинных опционов колл и пут. Эта позиция очень привлекательная, поскольку может быть прибыльной при движении базового инструмента на достаточную величину в любом направлении, и в то же время принесет прибыль при повышении волатильности (это наше основное допущение). Более того, короткие опционы колл хеджируют данную позицию в случае, если базовая ценная бумага останется вялой.
Прибыльность этого календарного спрэда показана на Рисунке 6.18. Кривые — это прибыль на момент мартовского истечения, то есть на момент истечения опционов ближнего срока. Нижняя линия на графике демонстрирует результаты позиции, если волатильность останется неизменной на уровне 20%, в то время как верхняя линия иллюстрирует более хорошие результаты, в случае повышения волатильности до 25%.
Обратный спрэд и длинный стрэддл. Это еще две основные стратегии, используемые нами при покупке волатильности (то есть когда желательно иметь положительную вегу). Я не считаю, что при использовании этих стратегий следует беспокоиться насчет гамма-нейтральности. Когда эти две стратегии приобретают дельту, это означает: мы получаем прибыль, поскольку происходит движение базового инструмента. Нейтрализация ценового движения гораздо важнее для стратегий продажи волатильности — в этом случае крупное движение акции могло привести к большим убыткам. Но в текущем случае крупное движение полезно. Я считаю, что достаточно быть дельта-нейтральным при соответствующем риске, связанном с волатильностью.
Предположим, мы хотим создать обратный спрэд, поскольку считаем, что волатильность, в текущий момент составляющая 20% и находящаяся на нижней границе своего исторического интервала, может повыситься. Следующие данные описывают ситуацию на 2 января при цене акции «XYZ», равной 100, и волатильности 20%:

Решение системы этих уравнений дает дельта-нейтральную позицию с вегой, равной +10, то есть при росте волатильности мы получим $1000 на каждом пункте ее роста.
Дельта-нейтральность: 0.91х + 0.57у = 0
Вега-экспозиция: 0.079х + 0.18у = 10
Решая, получаем х = -48 и у = 76, то есть желаемой является следующая позиция:
Лонг 76 Март-100-колл
Шорт 48 Март-90-колл
Эта позиция — типичный обратный спрэд. Случайно оказалось, что эта позиция имеет достаточно небольшую гамму, хотя мы и не нейтрализовывали ее. Можно вычислить позиционную гамму данной позиции, равную +2.40, то есть, если базовый инструмент повышается на один пункт, позиционная дельта, изначально нейтральная, поднимется до 2.40, что означает становление позиции дельта-длинной на 240 единиц. С другой стороны, если базовый инструмент снижается на один пункт, дельта становиться равной -2.40, то есть позиция перейдет в состояние дельта-короткой на 240 единиц.
Чем выше растет базовый инструмент, тем сильнее возрастет дельта. Чем дальше база будет снижаться, тем больше снизится дельта. В конечном счете, у вас будет позиция с достаточно большой дельтой — либо положительная на растущем рынке, либо отрицательная на падающем рынке. Однако это «хорошая» проблема, поскольку после больших движений базового инструмента ваша позиция будет прибыльной. О позиции длинного стрэддла я имею точно такое же мнение: обнулять его гамму необязательно.
Если при торговле волатильностью с длинной стороны (то есть ее покупке) вы предпочитаете гамма- и дельта-нейтральную стратегию, советую использовать календарный спрэд, как это показано в недавнем примере.
Еще более сложные построения
Нейтральные позиции, описанные ранее, и гамма-, и дельта-нейтральные. Теоретически можно строить позиции, остающиеся нейтральными по отношению к такому числу переменных, какому вы хотите. Но в конечном счете, если вы собираетесь получать прибыль, придется допустить в отношении некоторых из них какой-то риск, если вы трейдер, платящий комиссионные. Только маркет-мейкеры могут оставаться нейтральными по отношению ко всем переменным, поскольку их намерение покупать по бид и продавать по оффер, не принимая никакого дополнительного риска.
Чтобы создать позицию, нейтральную по отношению к трем переменным, придется просто построить три уравнения с тремя неизвестными и решить эту систему уравнений. Например, можно пожелать быть нейтральным по отношению к гамме и времени (тэте), но по-прежнему иметь некоторый риск по волатильности.
Другой показатель риска, к использованию которого пришли трейдеры — «гамма гаммы» («gamma of the gamma»), показывает, как быстро меняется гамма при росте базовой ценной бумаги на один пункт. Таким образом, многие трейдеры, более склонные к теории, считают, что им нужен еще один показатель, способный помочь поддерживать нейтральность позиции по отношению к ценовым изменениям базовой ценной бумаги. Это лишь говорит о том, насколько важной они считают нейтральность в отношении цены.
Итак, гамма, гамма гаммы и вега — три показателя, которые можно использовать в своих уравнениях. Вам доступно в самом конце нейтрализовать дельту, как это делалось в предыдущих примерах. При этом вы получите позицию, очень нейтральную по отношению к ценовому движению, но все еще обладающую риском по волатильности, то есть риском, который мы хотим иметь в контексте данной главы.
Данную концепцию можно распространить еще дальше — например, до четырех уравнений с четырьмя неизвестными (гамма, время [тэта], волатильность [вега] и гамма гаммы), с нейтрализацией дельты в самом конце. Без использования необходимых арифметических уравнений получить характеристики такой позиции абсолютно невозможно.
Не вдаваясь в детали, скажем, что один из предыдущих примеров можно использовать для построения позиции, нейтральной по четырем переменным и имеющей риск по отношению к волатильности. Начнем с идеи продажи Март-95/Март-105-комбинации и с использования в качестве защиты Февраль-90/Февраль-100-комбинации. Как оказалось, на 2 января при цене акции «XYZ», равной 98, после нейтрализации необходимых компонентов позиция выглядела следующим образом.
Лонг 28 Февраль-90-пут
Шорт 145 Март-95-пут
Шорт 45 Март-105-колл
Лонг 82 Февраль-110-колл
Шорт 5400 акций «XYZ»
Эта позиция обладает следующими качествами.
Дельта-нейтральность
Гамма-нейтральность
Тэта-нейтральность
Нейтральность в отношении гаммы гаммы
Риск в отношении волатильности: $1000 на пункт
Позиция обладает риском в верхней стороне, но 82 длинных опциона колл в основном компенсируют риск 45 коротких опционов колл и 5400 коротких акций. В нижнем направлении риск очевиднее, поскольку 5400 коротких акций и 28 длинных опционов пут меньше абсолютного хеджа против всех коротких Март-95-пут.
Для мелких и средних инвесторов необязательно добиваться такой нейтральности, но данный пример показывает, что это возможно.
Обобщение
Нами завершен раздел об использовании «греков» для нейтрализации позиций, позволяющих точнее определять риск по волатильности, одновременно управляя им. На самом деле все это не слишком сложно, что и демонстрируют представленные примеры. Однако даже после этой подготовки следует понять, что и в этих позициях по-прежнему можно понести убытки, особенно в случае использования непокрытых опционов.
|



















