|
Фрэнсис Гальтон (1822-1911) был светским снобом и никогда не зарабатывал на жизнь, если не считать кратковременной службы в больнице, когда ему было около двадцати. Тем не менее, трудно представить себе более приятного и привлекательного человека. Он был двоюродным братом Чарлза Дарвина, изобретателем и неутомимым исследователем той части Африки, куда до него не ступала нога белого человека. Он внес плодотворный вклад в развитие стратегии риска, но сделал это за счет упорной приверженности порочным идеям.


Измерения были хобби Гальтона, его навязчивой идеей. Его девизом могло бы быть «Считайте всё, что можно». Он измерял и обсчитывал головы, носы, руки, ноги, фиксировал у разных людей рост и вес, цвет глаз, изменения цвета лица у посетителей лошадиных бегов, бесплодие наследниц и число случаев невнимания на лекциях. Он классифицировал проходящих по улице девушек по степени привлекательности, прокалывая карту в левом кармане, если встречал хорошенькую, и другую карту в правом кармане, встречая дурнушку. В его «Карте красоты» Британии первое место занимают Лондон-ки, а последнее абердинки. Он проанализировал 10 000 судебных приговоров и заметил, что большинство из них повторяются с интервалами в 3, 6, 9, 12, 15, 18 и 24 года, в то время как нет приговоров, повторяющихся через 17 лет, и очень мало повторяющихся через 11 и 13 лет. На выставке крупного рогатого скота он представил в табличной форме 800 предположений посетителей относительно веса одного быка и нашел, что «в среднем общественное мнение оказалось верным с точностью до одного процента».
Основанная им в 1884 году антропометрическая лаборатория занималась выполнением обмеров и фиксацией всех возможных размеров человеческого тела, включая отпечатки пальцев. Последние особенно заинтересовали Гальтона, потому что, в отличие от других характеристик человеческого тела, они не меняются в процессе старения человека. Опубликованная им в 1893 году книга объемом в 200 страниц, посвященная этому вопросу, вскоре легла в основу использования отпечатков пальцев полицейскими службами.
Страсть Гальтона к измерениям не оставила его и во время предпринятого им в 1849 году путешествия в ту часть Африки, где сейчас находится Намибия. Попав в селение готтентотов, он обнаружил «фигуры, которые довели бы английскую женщину до отчаяния, – фигуры, которые были бы посмешищем в кринолине». Одна из женщин особенно привлекла его внимание. Как человек науки, он, по его словам, был «чрезвычайно заинтересован в точном обмере ее форм». Не имея возможности объясниться с готтентотами и не зная, что предпринять для проведения этого крайне необходимого обследования, он все же нашел выход из положения:
Случайно мне на глаза попался мой секстант, и тотчас пришла в голову блестящая мысль воспользоваться им для выполнения обмеров. Я провел серию измерений ее фигуры с разных точек... затем нагло вытащил рулетку, измерил расстояние между мной и объектом и, получив таким образом расстояния и углы, вычислил нужные мне величины с помощью тригонометрии и логарифмов.
Гальтон был типичным британцем Викторианской эпохи, шагавшим по земле как по собственным угодьям. Как-то во время охоты в Африке у него возникли опасения, что местный вождь нападет на его бивак. Натянув на себя красную охотничью куртку, шапку и высокие сапоги, он взгромоздился на быка, атаковал самую большую хижину в деревне и принудил быка сунуться головой в хижину. Его бивак стали обходить стороной.
В другой деревне он позволил себе бестактность, отказавшись участвовать в церемонии, в ходе которой хозяин полощет горло и выплевывает остатки в лицо гостю. Как-то король Нангоро подарил ему принцессу Чапангу на вечерок. Когда она пришла к нему, «вымазанная красной охрой и маслом», Гальтон ужаснулся. «Я был в моем единственном приличном белом льняном костюме и выпроводил ее с минимумом церемоний».
Королю Нангоро трудно было поверить, что в мире есть места, населенные людьми с белой кожей. Гальтон и его друзья казались ему редкими кочующими животными или какой-то аномалией. Одному из спутников Гальтона неоднократно приходилось раздеваться перед королем, чтобы убедить его, что у него вся кожа белого цвета. Любопытство Гальтона было ненасытным. Как-то, когда через Кембридж, где он тогда учился, проходил бродячий цирк, он вошел в клетку со львом; за всю историю этого цирка такое позволили себе только четыре человека. В студенческие годы он любил заниматься ночью и, чтобы не спать, надевал себе на голову «соображалку» – сложную конструкцию, время от времени подающую к голове холодную воду. Позднее он изобрел приспособление для чтения под водой и чуть не утонул в собственной ванне, увлекшись книгой.
Скоро вы узнаете, какие ужасные последствия имело увлечение Гальтона измерениями и выдумками. Тем не менее, ему мы обязаны крупным вкладом в развитие статистики и управления риском. Проверяя, подобно Кардано, свои идеи на опыте, он способствовал созданию новой статистической теории, хотя вовсе не ставил перед собой этой задачи.
Гальтон вводит нас в мир повседневности, где люди дышат, потеют, совокупляются и размышляют о будущем. В отличие от математиков прежних времен мы не анализируем игры и не смотрим на звезды для проверки своих теорий. Гальтон брал уже готовые теории и пускал их в работу.
Хотя он никогда не ссылался на Бернулли, в его работах нашла отражение мысль сварливого швейцарца о том, что вероятность является важнейшим средством анализа болезней, умственных способностей и физической ловкости. Он шел по стопам Гранта и Прайса, которых больше интересовало устройство человеческого общества, нежели исследование природы. То, что сделали эти люди, в конце концов, привело к созданию набора средств для контроля за риском и оценки его в бизнесе и финансовой деятельности.
Гальтон вырос в обстановке материального благополучия и оживленной интеллектуальной деятельности. Его дед, Эразм Дарвин, был одним из самых известных врачей своего времени, интересы которого отнюдь не ограничивались медициной. Он, в частности, изобрел паром, использующий механическую тягу вместо животной, туалет со сливом, экспериментировал с ветряными мельницами и паровыми двигателями, написал поэму в 2000 строк с детальным описанием процесса воспроизводства множества растений под названием «Любовь растений» («The Loves of Plants»). В 1796 году, когда ему было 65 лет, Эразм опубликовал двухтомный труд под названием «Зоономия, или Теория наследственности» («Zoonomia, or the Theory of Generations»). Хотя эта книга, имевшая сугубо теоретический характер, за семь лет выдержала три издания, она не получила должного отклика в научных кругах из-за скудости содержавшегося в ней фактического материала. Тем не менее «Зоономия» имеет поразительное сходство с «Происхождением видов» («The Origin of the Species»), опубликованным 63 года спустя его более знаменитым внуком Чарлзом Дарвином.
Гальтон рассказывал, что в четыре года он мог читать любую книгу, написанную на английском. Он декламировал наизусть «латинские существительные, прилагательные и все активные глаголы, а кроме того, 52 строки латинских стихов» и умел умножать на 2, 3, 4, 5, 6, 7, 10.
В 16 лет он начал изучать медицину в Бирмингеме, но описал посещение палат и морга как «ужас-ужас-ужас!». После того как Чарлз Дарвин порекомендовал ему «подзаняться математикой», он направился в Кембридж изучать математику и филологию.
Ему было 22 года, когда умер его отец, оставив своим семерым детям приличное состояние. Решив, что теперь можно делать все, что вздумается, он вскоре бросил учебу и, воодушевленный путешествием Дарвина на Галапагосские острова, предпринял свое первое путешествие в Африку. Он поднялся вверх по Нилу, а затем на верблюдах добрался до Хартума, пройдя в общей сложности более тысячи миль. Вернувшись домой, он четыре года бездельничал, а потом совершил второе путешествие в Африку. В 1853 году он написал книгу об Африке, получившую признание в научных кругах, после чего был принят в члены Королевского Географического общества, наградившего его золотой медалью, а в 1856 году стал членом Королевского общества.
Это предпринятое в 27 лет второе путешествие привело Гальтона к «расстройству здоровья» и приступам депрессии, повторявшимся довольно часто на протяжении всей его жизни. Он говорил, что во время этих приступов у него «вывихнутые мозги».
Гальтон был ученым-дилетантом, проявлявшим глубокий интерес к проблемам наследственности, но совершенно равнодушным к экономике и бизнесу. Тем не менее, его работы, касающиеся «идеального среднего дочернего типа», «родительского типа» и «усредненного наследственного типа», привели к открытиям в области статистики, имеющим существенное значение для прогнозирования и управления риском.
Наука о наследственности занимается изучением передачи из поколения в поколение таких ключевых характеристик, как умственные способности, цвет глаз, рост, манера поведения и пр. Всегда интересны исключения – индивидуумы, чьи характеристики не соответствуют норме, – но еще интереснее то, что все члены вида в значительной степени похожи друг на друга. Тенденция к усреднению, таящаяся за этой тенденцией к однородности, является важнейшей статистической закономерностью, имеющей отношение ко многим аспектам управления риском.
Гальтон пытался выяснить, как талант упорно сохраняется из поколения в поколение в некоторых семьях, в частности в его семье и в семье Бернулли. Он надеялся на сохранение таланта в собственном потомстве, но они с супругой оказались бездетными, так же как двое из его братьев и одна из сестер. Он очень старался выявить «черты природного благородства» у членов семей, которые он считал наиболее одаренными.
В 1883 году он назвал предмет своих ученых занятий евгеникой; греческий корень этого слова означает «хорошее» или «благое». Использование этого термина полстолетия спустя нацистами ассоциируется с уничтожением миллионов людей, которых они сочли бездарными и малоценными.
Вопрос о том, насколько Гальтон ответствен за эти преступления, был предметом острых дискуссий. Ничто не указывает на то, что он мог бы одобрить столь варварское поведение. Для него хорошее общество – это общество, признающее свою обязанность помогать «высокоодаренным» индивидуумам получать образование вне зависимости от их материального благосостояния, социальной и расовой принадлежности. Он предлагал приглашать и обустраивать в Британии «эмигрантов и спасающихся бегством» и способствовать тому, чтобы их потомки становились гражданами страны. В то же время он размышлял о путях ограничения рождаемости менее способных или больных людей, утверждая, что хорошее общество должно быть обществом, «в котором слабые могут найти приют и убежище в монастырях или сестринских общинах».
Невзирая на спорные трактовки труда Гальтона по евгенике, следует признать, что его значение выходит далеко за пределы прямо поставленных в нем вопросов. В сущности, это очередное подтверждение трюизма, что разнообразие придает вкус. Отдавая должное Клеопатре, римский военачальник Энобарбус заметил: «Возраст не лишает ее свежести, а бесконечное разнообразие делает ее неизменно привлекательной». Оставаясь самой собой, она была попеременно влюбленной, дружелюбной, холодной, горячей, соблазнительной, враждебной, покорной, требовательной. Человек может быть разным.
Каждый из живущих ныне 6 миллиардов людей является индивидуальностью. В вермонтских лесах растет несчетное количество кленов, каждый из которых отличается от других, но ни один из них нельзя спутать с березой или сосной. Акции General Electric, как и акции Biogen, одинаково просто купить на Нью-Йоркской фондовой бирже, но факторы риска для этих акций не имеют между собой ничего общего.
Какой из многочисленных ликов Клеопатры, кто из миллиардов ныне живущих людей, какой клен, какая береза или сосна в вермонтских лесах, какая акция на Нью-Йоркской бирже является типичным представителем своего вида? Насколько представители каждого вида отличаются друг от друга? Насколько младенец из Уганды отличается от старушки из Стокгольма? Есть ли в различиях закономерность, или они являются просто результатом случайных воздействий? Иначе говоря, что мы называем нормой?
В поисках ответов на такие вопросы Гальтон не использовал достижения математики и игнорировал специалистов по социальной статистике, подобных Гранту. Однако он ссылался на серию эмпирических исследований, выполненных в 1820-х и 1830-х годах бельгийским ученым Ламбертом Адольфом Жаком Кветеле (Quetelet), который был на двадцать лет старше Гальтона, приобрел известность как настойчивый исследователь устройства общества и был одержим измерениями не менее самого Гальтона.
Кветеле было всего 23 года, когда он получил степень доктора в новом университете в Генте. К этому времени он уже отдал дань изучению искусства, писал стихи и был соавтором оперы.
Он был, пользуясь выражением историка статистики Стивена Стиглера, «в равной степени ученым и организатором науки». Он принял участие в создании нескольких статистических ассоциаций, включая Лондонское Королевское статистическое общество и Международный статистический конгресс, и многие годы был региональным корреспондентом Бельгийского правительственного статистического бюро. Около 1820 года он возглавил кампанию за основание новой обсерватории в Бельгии, хотя его познания в астрономии в то время оставляли желать лучшего. После создания обсерватории он убедил правительство командировать его на три месяца в Париж для изучения астрономии и метеорологии и стажировки в Парижской обсерватории.
Во время пребывания в Париже он встречался со многими ведущими французскими астрономами и математиками, в результате чего приобрел хорошие познания в теории вероятностей. Он мог даже встретиться с завершавшим работу над последним томом своей «Mecanique celeste» («Небесной механики») Лапласом, которому было в ту пору 74 года. Кветеле был очарован теорией вероятностей и написал о ней три книги подряд, последнюю в 1853 году. Кроме того, он нашел хорошее практическое применение своим новым познаниям.
После возвращения из Парижа в 1820 году он, не оставляя работу в Королевской обсерватории в Брюсселе, проводил исследования, касающиеся народонаселения Франции, и готовился к предстоящей переписи 1829 года. В 1827 году была опубликована его монография, озаглавленная «Исследование населения, рождений, смертей, тюрем, приютов для бедных и т. п. в Королевстве Нидерланды» («Researches on population, births, deaths, prisons, and poor houses, etc. in the Kingdom of the Low Countries»), в которой Кветеле провел критический разбор процедур, используемых при сборе и анализе статистических данных. Ему не терпелось применить метод определения численности населения, разработанный Лапласом еще для переписи 1780-х годов во Франции. Этот метод сводился к обследованию случайных выборок из различных групп населения тридцати департаментов и использованию этих выборок в качестве основы для подсчета общей численности населения.
Коллеги скоро отговорили Кветеле от использования этого подхода. Дело в том, что чиновники, проводившие перепись, не знали, насколько репрезентативны эти выборки. В каждой местности были свои условия и обычаи, оказывавшие влияние на рождаемость. Более того, как отмечали еще Галлей и Прайс, на качество переписи даже в небольшом регионе может оказать сильное влияние перемещение населения. В отличие от Энобарбуса Кветеле счел, что структура народонаселения Франции слишком неоднородна, чтобы делать обобщения на основе выборочного обследования. Было решено провести сплошную перепись населения Франции.
Это заставило Кветеле заняться поисками объяснения различий между местностями и группами населения – откуда это разнообразие, придающее вкус жизни? Если различия случайны, данные должны выглядеть одинаково для каждой выборки, если же они закономерны, то выборки должны отличаться одна от другой.
Эта идея побудила Кветеле окунуться в оргию измерений, которую Стиглер описывал следующим образом:
Он обследовал рождения и смерти по месяцам и городам, в зависимости от температуры воздуха и времени дня... Он исследовал смертность по возрастам, по профессиям, по местностям, по сезонам, в тюрьмах и больницах. Он учитывал рост, вес, скорость роста и физическую силу... [и вел] статистический учет пьянства, сумасшествия, самоубийств и преступности.
В результате в 1835 году появился «Трактат о человеке и развитии его способностей» («A Treatise on Man and the Development of his Faculties»), вскоре переведенный на английский язык. Словом «faculties» («способности») переведено использованное Кветеле французское выражение physique social. Эта работа составила Кветеле имя. Автор трехчастной статьи в ведущем научном журнале заметил: «Мы рассматриваем появление этого тома как вступление в новую эпоху писаной истории цивилизации».
Книга представляет собой нечто большее, нежели просто набор сухих статистических данных и тяжеловесного текста. Кветеле создал героя, который жив до сих пор: Inhomme moyen, или средний человек. Новое понятие покорило воображение публики и принесло огромную известность его создателю.
Кветеле старался определить характеристики среднего мужчины (в некоторых случаях женщины), становившегося затем образом определенной группы, которую он представлял, будь то группа преступников, пьяниц, солдат или мертвецов. Кветеле даже теоретизирует, что, «если бы индивидуум на каком-нибудь этапе развития общества представлял все качества среднего человека, в нем отразилось бы все великое, доброе и прекрасное»15.
Не все были с этим согласны. Одним из самых суровых критиков книги Кветеле стал Антуан Августин Карно, знаменитый математик и экономист, большой авторитет в области теории вероятностей, утверждавший, что, не принимая во внимание законы вероятности, «мы не можем получить ясной оценки точности измерений, предлагаемых наукой о наблюдениях... или условий, ведущих к успеху коммерческих предприятий»16. Карно высмеял концепцию среднестатистического человека. Усреднением набора прямоугольных треугольников мы не получим прямоугольного треугольника, заметил он, а средний человек должен бы представлять собой некое чудовище.
Кветеле был непреклонен. Он был убежден, что сможет найти образ среднего человека для любой возрастной группы, рода занятий, места проживания или этнической принадлежности. Более того, он утверждал, что может не только определить, но и объяснить, почему данный индивидуум принадлежит скорее к одной группе, нежели к другой. Это был принципиально новый шаг: до сих пор еще никому не приходило в голову использовать математику и статистику для отделения причины от следствия. «Следствие пропорционально причине, – написал он и продолжил курсивом: – Чем большее число индивидуумов подвергается наблюдению, тем больше проявляются превалирующие характерные качества, физические или моральные, позволяющие выявить общие доминирующие факты, благодаря которым общество существует и сохраняется»". К 1836 году Кветеле развил эти идеи в книге о применении теории вероятностей в «моральных и политических науках».
Работа Кветеле о причинах и следствиях представляет собой увлекательное чтиво. Например, в ней можно найти подробный анализ факторов, влияющих на долю осужденных среди тех, кому предъявлено обвинение. В среднем 61,4% всех обвиняемых были осуждены, но вероятность обвинительного приговора в случае преступлений против личности составляла менее 50%, в то время как вероятность осуждения по обвинению в имущественных преступлениях составила свыше 60%. Вероятность осуждения была ниже 61,4%, если обвиняемыми оказывались женщины старше тридцати лет, грамотные и хорошо образованные, которые добровольно являлись в суд, вместо того чтобы уклоняться от него. Кветеле старался определить, являются ли отклонения от среднего значения 61,4% значимыми или случайными: он искал моральной достоверности в процессах над аморальностью.
Что бы ни брался исследовать Кветеле, всюду он видел колоко-лообразную кривую. Почти всегда «ошибки» или отклонения от среднего послушно распределялись согласно описанному Лапласом и Гауссом нормальному закону, симметрично уменьшаясь по обе стороны от среднего значения. Эта замечательно сбалансированная упорядоченность с пиком, соответствующим среднему значению, убеждала Кветеле в правомерности его излюбленного понятия среднего человека. Оно положено в основу всех его выводов, полученных на основе статистических обследований.
Например, в одном из обследований проводились измерения объема грудной клетки 5738 солдат шотландской армии. Кветеле построил кривую распределения результатов обследования и сравнил его с теоретической нормальной кривой. Они почти идеально совпали.
К этому времени уже было установлено, что нормальное распределение, описываемое формулой Гаусса, имеет широкое распространение в природе; теперь подтвердилось, что оно может быть положено в основу описания социальных явлений и физических характеристик людей. Исходя из этого, Кветеле пришел к заключению, что совпадение нормального распределения с результатами обследования шотландских солдат указывает на то, что отклонения от среднего значения, скорее всего, не отражали систематических различий в исследуемой совокупности, а носили случайный характер. Другими словами, совокупность представлялась в основном однородной, и средний солдат шотландской армии является идеальным представителем всех шотландских солдат. Клеопатра была прежде всего женщиной.
Однако в одной из работ Кветеле совпадение с нормальным распределением оказалось несколько менее выраженным. Анализируя распределение 100 000 французских призывников по росту, он обнаружил большое число малорослых, не позволяющее признать распределение нормальным. Поскольку в то время малый рост служил основанием для освобождения от воинской службы, Кветеле сделал вывод, что в ходе обследования результаты измерений мошеннически искажались с целью получения освобождения.
Замечание Карно о том, что среднестатистический человек должен оказаться монстром, отражало его мнение, что теория вероятностей применима к анализу естественнонаучных данных, но не применима в анализе общества. Он утверждал, что совокупность людей допускает сколь угодно произвольную классификацию. В отличие от него Кветеле верил, что нормальное распределение измерений, относящихся к группе людей, свидетельствует только о случайном характере различий в группе испытуемых. Но Карно подозревал, что различия могут быть не случайными. Рассмотрим, например, как можно классифицировать число рождений мальчиков в течение года: по возрасту родителей, по географическому положению обследуемых регионов, по дням недели, по этнической принадлежности, по весу, по времени беременности, по цвету глаз или длине среднего пальца, и это далеко не исчерпывающий список. Как здесь с уверенностью сказать, какое дитя является среднестатистическим! Карно полагал, что невозможно установить, какие из этих данных следует считать значимыми, а какие случайными: «Одна и та же величина отклонения [от среднего значения] может служить основанием для различных суждений». Карно не учитывал того, что хорошо известно современной науке, а именно что результаты большинства подобных измерений физических данных человека напрямую зависят от питания, то есть что они также являются отражением и социального статуса обследуемых.
Сегодня статистики обозначают то, что вызвало неприятие Карно, «добычей данных». Они говорят, что, если мучить данные достаточно долго, можно доказать что угодно. Карно чувствовал, что Кветеле ступил на опасную почву широких обобщений на основе ограниченного числа наблюдений. Весьма вероятно, что другая серия наблюдений над группой того же размера может дать результаты, существенно отличные от полученных в первой серии.
Несомненно, увлеченность нормальным распределением завела Кветеле слишком далеко. Тем не менее, в свое время его работы сыграли огромную роль. Позже знаменитый математик и экономист Фрэнсис Исидор Эджворт употребил термин «кветелизм» для обозначения повального увлечения нахождением нормальных распределений там, где их не было, или идеи считать нормальным любое распределение, далеко не отвечающее требованиям, предъявляемым нормальному распределению.
Первая работа Кветеле, с которой Гальтон впервые познакомился в 1863 году, произвела на него неизгладимое впечатление. «Среднее – это всего лишь единичный факт, – писал он, – тогда как при добавлении другого единичного факта начинает проявляться действующая нормальная схема, хорошо согласующаяся с данными наблюдений. Некоторые люди не переносят само упоминание о статистике, я же нахожу в ней бездну красоты и занимательности».
Гальтон был очарован Кветеле, считая, что «самый любопытный теоретический закон об отклонениях от среднего» – нормальное распределение – оказался вездесущим и особенно удобным для описания результатов таких измерений, как измерения роста или грудной клетки. Самому Гальтону понравилась колоколообразная кривая распределения 7634 оценок по математике, которые были проставлены студентам Кембриджского университета на выпускном экзамене, ранжированных от самой высокой до «трудно сказать, насколько плохой». Он обнаружил схожее статистическое распределение экзаменационных оценок на вступительных экзаменах в Королевский военный колледж в Сандхерсте.
Больше всего колоколообразная кривая привлекала Гальтона тем, что выявляла определенные наборы данных, которые могли рассматриваться как относительно однородные. И наоборот, отсутствие нормального распределения свидетельствовало о «неоднородности системы». Гальтон любил сильные высказывания: «Это предположение не может быть опровергнуто».
Но Гальтон искал как раз различия, а не однородность, – ему нужна была Клеопатра, а не среднестатистическая женщина. В рамках создаваемой им евгеники он искал различия даже в пределах групп, где измеряемые качества, казалось, укладывались в нормальное распределение. Гальтон ставил своей целью классификацию людей по «природным способностям», которые он понимал следующим образом:
...такие качества интеллекта и предрасположенности, которые побуждают человека и делают его способным совершать действия, ведущие к славе... Я имею в виду натуры, которые, будучи предоставлены самим себе, побуждаемые врожденными стимулами, карабкаются по тропе, ведущей на вершину, и имеют достаточно сил добраться до нее... Люди, достигшие вершины, и другие, по природе своей способные на это, в значительной
Гальтон начал с фактов. С 1866-го по 1869 год он собрал массу фактов для доказательства того, что таланты и достижения являются наследственными качествами. Потом он суммировал результаты поисков в самой значительной из своих работ «Наследственная одаренность», в приложение к которой включил отрывок из работы Кветеле, а также собственные едкие оценки неуживчивости, характерной для мужчин из семьи Бернулли. Книга начинается с оценки доли той части населения, которую Гальтон считает возможным охарактеризовать как «выдающуюся». На основе некрологов из «London Times» и биографического справочника он подсчитал, что в Британии того времени на 4000 или 5000 англичан среднего возраста приходилась одна знаменитость.
Хотя Гальтон говорил, что его не занимают люди со способностями ниже среднего уровня, он все же оценил, что на двенадцать миллионов англичан приходится 50 000 «идиотов и слабоумных», или один на 400, то есть в десять раз больше, чем одаренных граждан. Впрочем, интересовали его только одаренные. «Я уверен, – заключил он, – что никто не может сомневаться в существовании высших человеческих особей, по природе своей наделенных врожденным благородством, рожденных быть королями среди людей». Гальтон не игнорировал «очень одаренных женщин», но считал, что, «может быть, и хорошо для другого пола, что одаренная женщина – это большая редкость».
Гальтон был убежден, что если результаты измерений роста и грудной клетки подтверждают гипотезу Кветеле, то так же обстоит дело и с размерами черепной коробки, весом головного мозга и нервными волокнами, как, впрочем, и с интеллектуальными способностями. Он показал, как хорошо выводы Кветеле согласуются с его собственными оценками распределения способностей британцев: от одаренности с одной стороны до идиотизма с другой. Он пришел к «неоспоримому, но неожиданному заключению, что люди с выдающимися дарованиями настолько же выше людей среднего уровня, насколько последние выше идиотов».
Но кроме всего этого, Гальтон хотел доказать, что источником выдающихся талантов является только наследственность, а не «домашнее воспитание, не школа или университет и не профессиональная карьера». И кажется, действительно дело в наследственности, по крайней мере если речь идет о параметрах, избранных Гальтоном. Он, например, обнаружил, что каждый девятый из близких родственников 286 судей был отцом, сыном или братом другого судьи, в то время как доля судей в общей численности населения несравненно меньше 1/д. Более того, он выяснил, что многие родственники судей являются адмиралами, генералами, писателями, поэтами и врачами Ч (Гальтон явно исключал служителей церкви из числа одаренных людей.) Он был вынужден с разочарованием отметить, что в его выборке в неразделимой связке оказываются одаренные люди и «конгенитальные идиоты».
Однако Гальтон установил, что высокие способности сохраняются в семье ненадолго, или, как говорят физики, имеют короткий период полураспада. Он обнаружил, что только 36% сыновей именитых людей сами достигали высокого положения, а внукам это удавалось только в 9% случаев. Он пытается объяснить, почему именитые фамилии имеют тенденцию к вымиранию, ссылаясь на общеизвестный обычай жениться на наследницах. Чем они виноваты? Потому что наследницы должны происходить из неплодовитых семей, утверждает Гальтон; если бы они имели большое число братьев и сестер, фамильное состояние делилось бы на всех и они не имели бы статуса «наследниц». Это было неожиданное утверждение в устах человека, который жил в комфорте после того, как поделил наследство своего отца с шестью братьями и сестрами.
«Гальтон наверняка счел бы Кардано выдающейся личностью, но что он должен был бы подумать о его несчастном потомстве? С Гауссом, тоже выдающимся человеком, дело обстоит получше, пятеро из его детей выжили; один стал известным инженером, а двое эмигрировали в Соединенные Штаты, чтобы стать удачливыми бизнесменами (а также сбежать от подавляющего влияния своего отца); один из них был одновременно блестящим лингвистом, игроком и искусным математиком.
«Не думаю, что мне приходилось читать что-нибудь более интересное и оригинальное... примечательная книга». Дарвин советовал продолжить анализ статистических данных о наследственности, но Гальтона не нужно было подстегивать. Дело по разработке новой науки евгеники шло полным ходом, и он был полон страстного желания выявить и сохранить то, что он называл лучшим в человечестве. Гальтон хотел, чтобы лучшие люди имели больше потомства, а бездарности проявляли сдержанность.
Но на его пути упорно стоял закон об отклонениях от среднего. Нужно было как-то объяснить различия внутри нормального распределения. Гальтон понимал, что прежде всего для этого нужно выяснить, почему данные распределяются по колоколообразной кривой. Поиски ответа на этот вопрос привели его к потрясающему открытию, влияющему ныне на принятие большинства решений, больших и малых.
О первом шаге Гальтон сообщил в статье, которая была опубликована в 1875 году; в ней он высказал предположение, что универсальность симметричного распределения относительно среднего значения может быть результатом влияний факторов, которые сами распределены нормальным образом, выстраиваясь от наиболее редких условий к наиболее частым и затем опять к наиболее редким противоположным условиям. Гальтон предположил, что даже в рамках каждого отдельного фактора влияние распределяется от самого слабого к сильному и затем опять к противоположному слабому. Суть его аргументации сводилась к тому, что «посредственные» влияния встречаются гораздо чаще, чем экстремальные, неважно, плохие или хорошие.
Гальтон продемонстрировал модель своей идеи в Королевском обществе в 1874 году с помощью приспособления, которое он назвал quincunx (Квинкункс – математическое понятие, означающее расположение элементов по углам прямоугольника или квадрата с пятым элементом в центре. – Примеч. переводчика). Это нечто вроде игры в пинбол: наклонная доска с узкой горловиной вверху, как у песочных часов, с торчащими пониже горловины двенадцатью штырьками. На противоположном широком конце лотка ряд небольших ячеек. Стоит сыпануть дроби, и она, натыкаясь на штырьки, падает вниз, заполняя расположенные внизу ячейки в полном соответствии с распределением Гаусса – большая часть дробинок собирается в средних ячейках, остальные в убывающих количествах заполняют крайние.
В 1877 году во время выступления с большим докладом на тему «Основные законы наследственности» («Typical Laws of Heredity») Гальтон предложил новую модель своего приспособления. (Мы не знаем, построил ли он ее на самом деле.) В этой модели на пути дробинок после горловины устанавливались такие же ячейки, как на дне первой модели, но с отверстием на дне, до поры закрытым. Когда отверстие на дне какой-либо из этих верхних ячеек открывалось, дробинки скатывались в нижние ячейки, где и располагались, как вы уже, наверное, догадались, по закону нормального распределения.
Потрясающее открытие! Свойства любой группы, сколь угодно малой и хоть как-то отличающейся от других групп, имеют тенденцию распределяться в соответствии с колоколообразной кривой, так что большая часть группы попадает близко к центру, или, как принято говорить, к среднему. Когда все группы сливаются в одну, как это было в первом варианте модели, дробинки также располагаются в соответствии с нормальным распределением. Таким образом, нормальное распределение большой группы выявляет среднее от средних значений для малых подгрупп.
Вторая механическая модель была упрощенным воплощением идеи, к которой Гальтон пришел по ходу эксперимента, предложенного Дарвином в 1875 году. В этом эксперименте не использовались кости, звезды и даже люди. Использовался сладкий стручковый горох. Сладкий горох хорошо хранится, плодовит и имеет слабую тенденцию к перекрестному опылению. В каждом стручке горошины почти одинакового размера. Взвесив и пересчитав тысячи сладких горошин, Гальтон разослал десять партий по семь упаковок разного веса, в каждой девяти друзьям, включая Дарвина, жившим в разных концах Британии, с подробными инструкциями, касающимися посадки и выращивания гороха в разных условиях.
Проанализировав результаты, Гальтон сообщил, что потомство от каждой из семи партий по весу в точности повторило распределение, которое предсказало бы его приспособление. Веса горошин, выращенных из каждой из семи упаковок внутри каждой партии, образовывали нормальное распределение, и веса горошин, выращенных из каждой партии, также образовали нормальное распределение. Этот убедительный результат не был, как сказал Гальтон, следствием «разных комбинаций незначительных влияний» [курсив Гальтона. – П.Б.]. Скорее, «процессы наследования... находятся под действием не малых, а очень важных влияний». Подобно тому, как немногие индивидуумы в группе людей оказываются одаренными, среди их отпрысков также немногие отличаются заметными талантами; поскольку большинство людей имеют средние способности, их потомки также обречены на средний уровень. Посредственность всегда многочисленнее талантов. Последовательность малых-больших-малых размеров горошин, образующая нормальное распределение, убедила Гальтона, что доминирующим фактором, определяющим свойства потомства, являются качества родителей.
Как свидетельствует приведенная ниже таблица распределения горошин первого и второго поколений по диаметру, эксперимент выявил кое-что еще.
Диаметр высеянных горошин и их потомства» (в сотых долях дюйма)
Исходные горошины 15 16 17 18 19 20 21
Средний диаметр горошин второго поколения 15,4 15,7 16,0 16,3 16,6 17,0 17,3
Заметьте, что разброс диаметров среди родительских семян больше, чем у потомства. Средний диаметр родительских горошин был 0,18 дюйма с разбросом от 0,15 до 0,21 дюйма, или по 0,03 дюйма справа и слева от среднего значения. Средний диаметр выращенных горошин оказался равным 0,163 дюйма с разбросом от 0,154 до 0,173 дюйма, или по 0,01 дюйма справа и слева от среднего значения. Потомство распределено в более узком интервале, чем родительское поколение.
На основе этого эксперимента Гальтон предложил общий принцип, получивший название регрессии, или схождения к среднему. «Схождение, – писал Гальтон, – это тенденция идеально среднего второго поколения отойти от родительского типа, возвращаясь к тому, что можно грубовато, но, по-видимому, верно назвать усредненным наследственным типом». Если бы этот процесс схождения не срабатывал, то есть если бы (в нашем случае) большие горошины продуцировали бы еще большие, а малые – еще меньшие, то в мире не осталось бы никого, кроме карликов и гигантов. Природа из поколения в поколение становилась бы все более причудливой, стремясь к абсолютной нестабильности или выходя за такие пределы, о которых не хочется и думать.
Гальтон подытожил результаты этих исследований в одном из своих наиболее красноречивых и выразительных высказываний:
Ребенок наследует частично от своих родителей, частично от их предков... Чем дальше мы возвращаемся назад по его генеалогическому древу, тем большее число предков и вариаций выявляется в его наследственности, пока они не перестанут отличаться от столь же многочисленной случайной выборки, произвольно взятой из расы... Этот закон наносит сильный удар по представлениям о простом наследовании какого-либо таланта. <...> Закон симметричен: он касается наследования как пороков, так и добродетелей. Охлаждая экстравагантные надежды одаренных родителей на то, что их дети унаследуют все их таланты, он не менее убедительно рассеивает их опасения относительно возможного наследования их слабостей и болезней.
Элегантность формулировки не могла сделать этот вывод приятным для Гальтона, но он стимулировал его усилия по разработке евгеники. Само собой напрашивалось решение усилить влияние «усредненного наследственного типа» за счет ограничения воспроизводства потомства на нижнем конце шкалы; нужно было просто отсечь левую ветвь нормального распределения.
Гальтон нашел еще одно подтверждение схождения к среднему в эксперименте, о котором он рассказал в 1885 году по случаю его избрания президентом Британской ассоциации развития науки. Для этого эксперимента он собрал огромное количество данных о людях, которые он получил в ответ на публичное предложение снабдить его информацией за определенную плату. Он проанализировал данные о 928 взрослых детях, рожденных от 205 родительских пар.
На этот раз Гальтон занялся сравнением роста родителей и детей. Так же как и в эксперименте со сладким горошком, он и в этом обследовании поставил своей целью проверить, как это частное свойство передается по наследству. Чтобы скорректировать для целей анализа различие в росте между мужчинами и женщинами, он умножал рост женщины на 1,08, складывал показатели роста обоих родителей и делил на два. Он назвал эту величину «средним ростом родителей». Ему нужно было также быть уверенным в отсутствии тенденции к женитьбе высоких мужчин на высоких женщинах, а маленьких на маленьких; его вычисления были «достаточно скрупулезны», чтобы исключить наличие такой тенденции.
Соотношение между ростом 928 взрослых детей и ростом 205 родительских пар
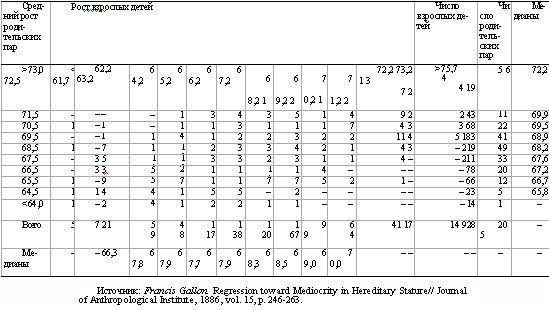
Как видно из таблицы, результат получился великолепный. Структура чисел по диагонали от левого нижнего угла до правого верхнего показывает, что у высоких родителей вырастают высокие дети и наоборот – наследственность имеет значение. Группы больших чисел в центральной части таблицы позволяют сделать вывод, что распределение детей по росту является нормальным и что рост детей, родители которых относятся к одной группе роста, также описывается нормальным распределением. И наконец, сравним самую правую и самую левую колонки. («Медиана» означает, что в половине группы люди были выше, а в половине – ниже этого числа.) Дети всех родителей, средний рост которых был выше 68,5 дюйма, в среднем оказались ниже своих родителей; дети всех родителей, средний рост которых был ниже 68,5 дюйма, в среднем оказались выше своих родителей. Совсем как в эксперименте со сладким горошком.
Упорядоченность нормального распределения и наличие сходимости позволили Гальтону вычислить другие показатели – например, долю высоких родителей, дети которых выше своих сверстников, но ниже родителей. Когда профессиональные математики подтвердили его результаты, Гальтон написал: «Я еще никогда не испытывал такого глубокого уважения к величественной и непререкаемой власти математического анализа».
Подход Гальтона в конце концов привел к разработке понятия корреляции, которая измеряет, насколько тесно связаны между собой изменения двух величин, будь то размеры родителей и детей, количество осадков и урожай, инфляция и процентные ставки или цены на акции General Motors и Biogen.
Карл Пирсон, главный биограф Гальтона и сам выдающийся математик, заметил, что Гальтон совершил «революцию в наших научных представлениях, [которая] изменила философский подход к науке и даже к самой жизни». Это не преувеличение: идея схождения к среднему сработала как динамит. Гальтон превратил статическое понятие вероятности, базирующееся на случайности и законе больших чисел, в динамическую концепцию, описывающую процесс, в котором преемникам крайних предопределено присоединиться к толпе в центре. Изменение и движение от внешних границ к центру постоянно, неизбежно и предсказуемо. Учитывая динамические свойства этого процесса, нельзя и помыслить, что его результатом будет что-либо, кроме нормального распределения. Тенденция всегда направлена к среднему, к восстановлению «нормальности», к среднему, или среднестатистическому, человеку Кветеле.
Принцип схождения к среднему объясняет почти все разнообразие поведения в условиях риска и прогнозирования. Этот принцип сквозит в поговорках типа: «Не всё коту масленица», «С высоты больнее падать», «Карта не лошадь, к утру да придет». Именно эту предопределенность событий имел в виду Иосиф, когда предсказал фараону, что за семью тучными годами последуют семь тощих лет. Об этом же думал Д. П. Морган, когда говаривал, что «рынок переменчив». Это кредо так называемых контрапунктных инвесторов, которые всегда работают в противофазе: когда они говорят, что цена акций завышена или занижена, то имеют в виду, что страх или жадность побудили толпу поддерживать цену на акции, не соответствующую их внутренней ценности, к которой цена непременно вернется со временем. Именно на это уповает проигрывающий игрок – карта не лошадь, к утру да придет. Именно это имеет в виду мой врач, когда говорит, что «потерпи» и всё пройдет. И именно с этой точки зрения воспринимал события Герберт Гувер, когда в 1931 году, ободряя сограждан, говорил, что процветание уже за углом, – к несчастью для него и других, он был не прав, середина находилась не там, где он предполагал.
|



















